
【题目】如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
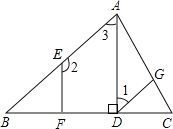
解:因为AD⊥BC,EF⊥BC(______ )
所以∠ADC=90°,∠EFD=90°(______ )
得∠ADC=∠EFD(等量代换),
所以AD∥EF(______ )
得∠2+∠3=180°(______ )
由∠1+∠2=180°(______ )
得∠1=∠3(______ )
所以DG∥AB(______ )
所以∠CGD=∠CAB(______ )
【答案】已知 垂直定义 同位角相等,两直线平行 两直线平行,同旁内角互补 已知 同角的补角相等 内错角相等,两直线平行 两直线平行,同位角相等
【解析】
求出AD∥EF,根据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.绳子的形状近似成了抛物线![]() ,如图1,已知BD=8米,绳子最低点离地面的距离为1米.
,如图1,已知BD=8米,绳子最低点离地面的距离为1米.
(1)求立柱AB的长度;
(2)由于挂的衣服比较多,为了防止衣服碰到地面,小华用一根垂直于地面的立柱MN撑起绳子(如图2),MN的长度为1.85米,通过调整MN的位置,使左边抛物线F1对应函数的二次项系数为![]() ,顶点离地面1.6米,求MN离AB的距离.
,顶点离地面1.6米,求MN离AB的距离.
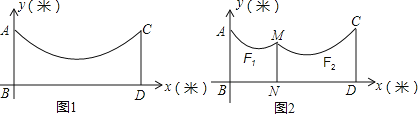
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩种植脐橙,投资59000元种植脐橙果树4000棵;今年脐橙总产量预测为60000千克,脐橙在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售2000千克,需4人帮忙,每人每天付工资100元,农用车运费及其他各项税费平均每天300元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=2.5元,b=2元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
(3)该农户加强果园管理,力争到明年纯收入达到84000元,而且该农户采用了(2)中较好的出售方式出售,那么纯收入增长率是多少(纯收入=总收入﹣总支出)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算F,规定:F(x,y)=ax+by(其中a,b均为非零常数).例如:F(3,4)=3a+4b.
(1)已知F(1,﹣1)=﹣1,F(2,0)=4.
①求a,b的值;
②已知关于p的不等式组![]() ,求p的取值范围;
,求p的取值范围;
(2)若运算F满足![]() ,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com