
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,2),B(-4,0),C(-4;-4),
(1)在y轴右侧,以O为位似中心,画出△A'B'C′,使它与△ABC的相似比为1:2;
(2)根据(1)的作图,sin∠A'C'B′=__________.

科目:初中数学 来源: 题型:
【题目】某花卉种植基地准备围建一个面积为100平方米的矩形苗圃园种植玫瑰花,其中一边靠墙,另外三边用29米长的篱笆围成.已知墙长为18米,为方便进入,在墙的对面留出1米宽的门(如图所示),求这个苗圃园垂直于墙的一边长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
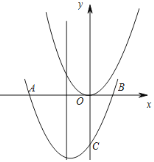
【题目】如图,在平面直角坐标系xOy中,将抛物线y=x2平移,使平移后的抛物线经过点A(–3,0)、B(1,0).
(1)求平移后的抛物线的表达式.
(2)设平移后的抛物线交y轴于点C,在平移后的抛物线的对称轴上有一动点P,当BP与CP之和最小时,P点坐标是多少?
(3)若y=x2与平移后的抛物线对称轴交于D点,那么,在平移后的抛物线的对称轴上,是否存在一点M,使得以M、O、D为顶点的三角形△BOD相似?若存在,求点M坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
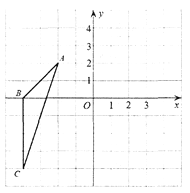
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,2),B(-4,0),C(-4;-4),
(1)在y轴右侧,以O为位似中心,画出△A'B'C′,使它与△ABC的相似比为1:2;
(2)根据(1)的作图,sin∠A'C'B′=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
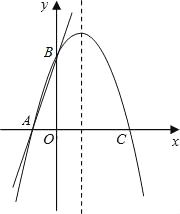
【题目】如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
(1)求抛物线的解析式;
(2)求抛物线的对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=30°,AC=8,∠B=90°,点D在AB上,BD=![]() ,点P在△ABC的边上,则当AP=2PD时,PD的长为____________________.
,点P在△ABC的边上,则当AP=2PD时,PD的长为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
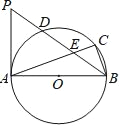
【题目】如图,AB是⊙O的直径,BC为弦,D为弧AC的中点,AC、BD相交于点E.AP交BD的延长线于点P.∠PAC=2∠CBD.
(1)求证:AP是⊙O的切线;
(2)若PD=3,AE=5,求△APE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
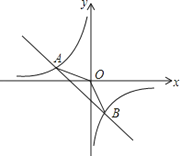
【题目】如图,在平面直角坐标系xOy中,一次函数y![]() =ax+b(a,b为常数,且a≠0)与反比例函数y
=ax+b(a,b为常数,且a≠0)与反比例函数y![]() =
=![]() (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com