练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD＝6，阴影部分图形的面积为（ ）

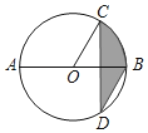
    A. 4πB. 3πC. 2πD. π

    【答案】C

    【解析】

    先求出△BOC是等边三角形，再根据垂径定理及圆周角定理得到∠CBO＝∠BOD，由S△BCD＝S△BCO将阴影部分面积转化为S扇形OBC，代入数值求解即可.

    解：连接BC，OD，设CD交AB于E．

    ∵∠BOC＝2∠CDB，∠CDB＝30°，

    ∴∠COB＝60°，

    ∵OC＝OB，

    ∴△BOC是等边三角形，

    ∴∠CBO＝60°，

    ∵CD⊥AB，CD＝6，

    ∴＝，CE＝ED＝3，

    ∴∠BOC＝∠BOD＝60°，EO＝，OC＝2，

    ∴∠CBO＝∠BOD，

    ∴BC∥OD，

    ∴S△BCD＝S△BCO，

    ∴S阴＝S扇形OBC＝＝2π．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了了解中学生的身体发育情况，对某一中学同年龄的50名女学生的身高进行了测量，结果如下(单位：厘米)：

    完成下面的频率分布表．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

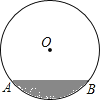
    【题目】在半径为17dm的圆柱形油罐内装进一些油后，横截面如图．

    （1）若油面宽AB=16dm，求油的最大深度．

    （2）在（1）的条件下，若油面宽变为CD=30dm，求油的最大深度上升了多少dm？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，对于平面上不大于的，我们给出如下定义：若点P在的内部或边界上，作于点E，．于点，则称为点P相对于的“优点距离”，记为

    如图2，在平面直角坐标系xOy中，对于，点P为第一象限内或两条坐标轴正半轴上的动点，且满足5，点P运动形成的图形记为图形G．

    （1）满足条件的其中一个点P的坐标是 __，图形G与坐标轴围成图形的面积等于 __ ；

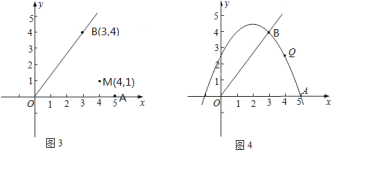
    （2）设图形G与x轴的公共点为点A，如图3，已知，，求的值；

    （3）如果抛物线经过（2）中的A，B两点，点Q在A，B两点之间的物线上（点Q可与A，B两点重合），求当取最大值时，点Q 的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解初一年级学生每学期参加综合实践活动的情况，某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：

    （I）本次随机抽样调查的学生人数为　 　，图①中的m的值为　 　；

    （II）求本次抽样调查获取的样本数据的众数、中位数和平均数；

    （III）若该区初一年级共有学生2500人，请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB＝AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F．

    （1）求证：DE是⊙O的切线；

    （2）若⊙O的半径为4，∠F＝30°，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．

    （1）画出△ABC关于x轴对称的△A1B1C1；

    （2）画出△ABC绕点O逆时针旋转90°后的△A2B2C2；

    （3）在（2）的条件下，求线段BC扫过的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列两则材料，回答问题：

    材料一：平面直角坐标系中，对点A（x1，y1），B（x2，y2）定义一种新的运算：AB=x1x2+y1y2．

    例如：若A（1，2），B（3，4），则AB=1×3+2×4=11

    材料二：平面直角坐标系中，过横坐标不同的两点A（x1，y1），B（x2，y2）的直线的斜率为kAB=．由此可以发现若kAB==1，则有y1-y2=x1-x2，即x1-y1=x2-y2．反之，若x1，x2，y1，y2满足关系式x1-y1=x2-y2，则有y1-y2=x1-x2，那么kAB=═1．

    （1）已知点M（-4，6），N（3，2），则MN=______，若点A，B的坐标分别为（x1，y1），（x2，y2）（x1≠x2），且满足关系式x1+y1=x2+y2，那么kAB=______；

    （2）横坐标互不相同的三个点C，D，E满足CD=DE，且D点的坐标为（2，2），过点D作DF∥y轴，交直线CE于点F，若DF=8，请结合图象，求直线CE与坐标轴围成的三角形的面积．

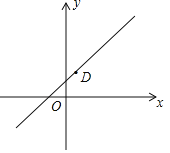
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】程大位是我国明朝商人，珠算发明家．他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法．书中有如下问题：

    一百馒头一百僧，大僧三个更无争，

    小僧三人分一个，大小和尚得几丁．

    意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人，下列求解结果正确的是（　　）

    A. 大和尚25人，小和尚75人 B. 大和尚75人，小和尚25人

    C. 大和尚50人，小和尚50人 D. 大、小和尚各100人

    查看答案和解析>>

    同步练习册答案