
【题目】将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在![]() 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠.
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠.
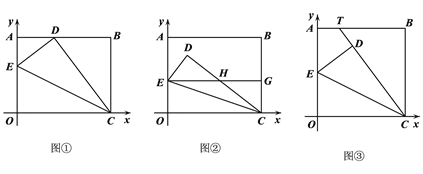
(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥![]() 轴交CD于点H,交BC于点G. 求证:EH=CH;
轴交CD于点H,交BC于点G. 求证:EH=CH;
(3)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度.
【答案】(1)(0,5);(2)证明见解析;(3)2.5.
【解析】试题分析:(1)根据翻折变换的性质以及勾股定理得出BD的长,进而得出AE,EO的长即可得出答案;
(2)利用平行线的性质以及等角对等边得出答案即可;
(3)首先得出Rt△ATE≌Rt△DTE进而得出AT=DT.设AT=x,则BT=10-x,TC=10+x,在Rt△BTC中,BT2+BC2=TC2,求出即可.
试题解析:(1)∵将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,点O落在AB边上的点D处,
∴OC=DC=10,
∵BC=8,
∴BD=![]() =6,
=6,
∴AD=10-6=4,
设AE=x,则EO=8-x,
∴x2+42=(8-x)2,
解得:x=3,
∴AE=3,
则EO=8-3=5,
∴点E的坐标为:(0,5),
故答案为:(0,5);
(2)∵EG∥x轴,∴∠OCE=∠CEH,
由折叠可知∠OCE=∠ECH,
∴∠CEH=∠ECH,
∴EH=CH;
(3)连接ET,
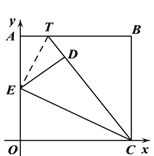
由题意可知,ED=EO,ED⊥TC,DC=OC=10,
∵E是AO中点,∴AE=EO,
∴AE=ED,
在Rt△ATE和Rt△DTE中,
![]() ,
,
∴Rt△ATE≌Rt△DTE(HL),
∴AT=DT,
设![]() ,则
,则![]() ,
, ![]() ,
,
在Rt△BTC中, ![]() ,
,
即![]() ,
,
解得![]() ,即
,即![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,以下说法错误的是( )
A. AC=2CDB. AD=2CDC. AD=3BDD. AB=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒).该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元.经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
(1)若这个班计划购买6盒乒乓球,则在甲商店付款 元,在乙商店付款 元;
(2)当这个班购买多少盒乒乓球时,在甲、乙两家商店付款相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG⊥AE于点G,交AD于点H,则下列结论错误的是( )

A. AH=DF B. S四边形EFHG=S△DCF+S△AGH
C. ∠AEF=45° D. △ABH≌△DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E.
(1)线段AB与DB的大小关系为___________,请证明你的结论;
(2)求证:CE 是⊙O的切线;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店积极响应政府“改革创新,奋发有为”的号召,举办“读书节“系列活动.活动中故事类图书的标价是典籍类图书标价的1.5倍,若顾客用540元购买图书,能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本.
(1)求活动中典籍类图书的标价;
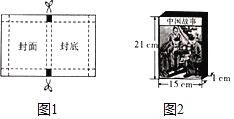
(2)该店经理为鼓励广大读者购书,免费为购买故事类的读者赠送图1所示的精致矩形包书纸.在图1的包书纸示意图中,虚线是折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长为折叠进去的宽度.已知该包书纸的面积为875cm2(含阴影部分),且正好可以包好图2中的《中国故事》这本书,该书的长为21cm,宽为15cm,厚为1cm,请直接写出该包书纸包这本书时折叠进去的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连结DF,DE, EF. 过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).

(1) 填空:当t= 时,AF=CE,此时BH= ;
(2)当△BEF与△BEH相似时,求t的值;
(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.
① 求S关于t的函数关系式;
② 直接写出周长C的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
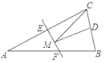
【题目】如图,等腰三角形ABC的底边BC长为6,面积是24,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com