
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E.
(1)线段AB与DB的大小关系为___________,请证明你的结论;
(2)求证:CE 是⊙O的切线;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明.

【答案】(1)AB=DB;(2)见解析;(3)△ABD为等边三角形,理由见解析
【解析】试题分析:(1)首先连接BC,由AB是⊙O的直径,可得∠ACB=90°,又由AC=CD,利用三线合一的知识,即可判定AB=DB;
(2)首先连接OC,由点O为AB的中点,点C为AD的中点,根据三角形中位线的性质,可证得OC∥BD,又由CE⊥BD,即可证得CE⊥OC,即得CE与⊙O的切线;
(3)易证得△CED∽△BCD,然后由相似三角形的对应边成比例证得:CD:BD=1:2,可求得∠CBD=30°,即可得∠D=60°,则可证得△ABD是等边三角形.
试题解析:(1)AB=DB,证明如下:
连结BC,∵AB是⊙O的直径,∴∠ACB=90°,即BC⊥AD,
又∵AC=CD,∴BC垂直平分线段AD,∴AB=DB;
(2)连接OC,
∵点O为AB的中点,点C为AD的中点,∴OC为△ABD的中位线,∴OC//BD,
又∵CE⊥BD,∴CE⊥OC,∴CE是⊙O的切线;
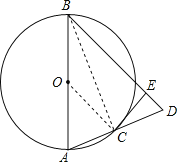
(3)△ABD是等边三角形,证明如下:
由![]() =
=![]() ,
,
得![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,∴
,∴![]() =
=![]() ,
, ![]() =
=![]() ,
,
∵∠D=∠D,∠CED=∠BCD=90°,∴△CED∽△BCD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
在Rt△BCD中,∵sin∠CBD=![]() =
=![]() ,
,
∴∠CBD=30°,∴∠D=60°,
又∵AB=DB,∴△ABD是等边三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
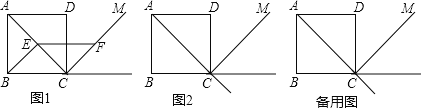
【题目】在正方形ABCD中,点E是射线AC上一点,点F是正方形ABCD外角平分线CM上一点,且CF=AE,连接BE,EF.
(1)如图1,当E是线段AC的中点时,直接写出BE与EF的数量关系;
(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否成立,并证明你的结论;
(3)当点B,E,F在一条直线上时,求∠CBE的度数.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AC=2,BD=2![]() ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
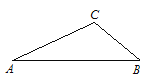
【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
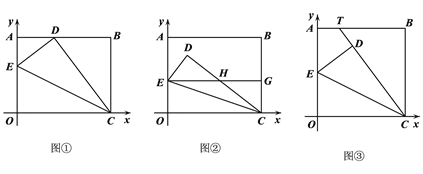
【题目】将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在![]() 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠.
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠.
(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥![]() 轴交CD于点H,交BC于点G. 求证:EH=CH;
轴交CD于点H,交BC于点G. 求证:EH=CH;
(3)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克.设每千克核桃应降价x元.
(1)降价后的每千克核桃的售价为 元,每天的销售量为 千克.
(2)如果该专卖店销售这种核桃要想平均每天获利2240元,同时尽可能让利于顾客,赢得市场,那么该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下)
(1)写出D级学生的人数占全班总人数的百分比为 ,C级学生所在的扇形圆心角的度数为 ;
(2)该班学生体育测试成绩的中位数落在等级 内;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎军运会,武汉市对城区主干道进行绿化,计划把某一段公路的两侧全部栽上银杏树,要求每两棵树的间隔相等,并且路的每一侧的两端都各栽一棵,如果每隔4米栽一棵,则还差102棵;如果每隔5米栽一棵,则多出102棵,设公路长x米,有y棵树,则下列方程中:①2(![]() +1)﹣102=2(
+1)﹣102=2(![]() +1)+102;②
+1)+102;②![]() ﹣102=
﹣102=![]() +102;③4(
+102;③4(![]() ﹣1)=5(
﹣1)=5(![]() ﹣1);④4(
﹣1);④4(![]() ﹣1)=5(
﹣1)=5(![]() ﹣1),其中正确的是( )
﹣1),其中正确的是( )
A.①③B.②③C.①④D.①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com