
【题目】已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于D、E.
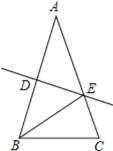
(1)若AC=12,BC=10,求△EBC的周长;
(2)若∠A=40°,求∠EBC的度数.
 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
B.到点![]() 距离等于
距离等于![]() 的点的轨迹是以点
的点的轨迹是以点![]() 为圆心,半径长为
为圆心,半径长为![]() 的圆
的圆
C.到直线![]() 距离等于
距离等于![]() 的点的轨迹是两条平行于
的点的轨迹是两条平行于![]() 且与
且与![]() 的距离等于
的距离等于![]() 的直线
的直线
D.等腰三角形![]() 的底边
的底边![]() 固定,顶点
固定,顶点![]() 的轨迹是线段
的轨迹是线段![]() 的垂直平分线
的垂直平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:
①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出![]() =83分,
=83分,![]() =82分,绘制成如下尚不完整的统计图表.
=82分,绘制成如下尚不完整的统计图表.
甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
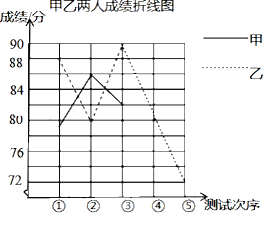
(1)a=
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 的图像过点
的图像过点![]() ,且与
,且与![]() 轴及
轴及![]() 的图像分别交于点
的图像分别交于点![]() 、
、![]() ,
,![]() 点坐标为
点坐标为![]() .
.
(1)求n的值及一次函数![]() 的解析式.
的解析式.
(2)求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:折纸中的数学
问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:
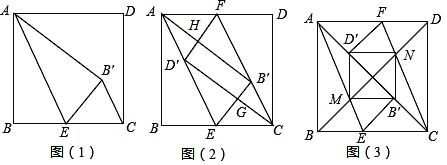
问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.
问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.
(1)解决问题:请你对兴趣小组提出的两个问题进行证明.
(2)拓展探究:解决完兴趣小组提出的两个问题后,实践小组的同学们进行如下实践操作:如图(3),点E,点F分别为BC、AD上的点,将正方形纸片沿AE、CF折叠,使得点B落在对角线上的点B′处,点D落在对角线AC上的点D′处,AE与对角线BD的交点为M,CF与对角线BD的交点为N,分别连接MB′,B′N,D′N,D′M.他们认为四边形MB′ND′为正方形.
实践小组的同学们发现的结论是否正确?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
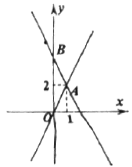
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com