
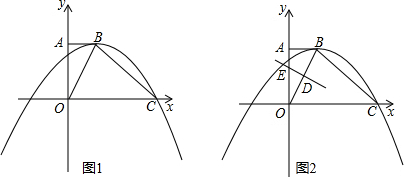
���� ��1���������B�����꣬���ö������깫ʽ���a��b��ֵ���ɵĽ���ʽ��
��2�����������ۣ�0��t��1��1��t��$\frac{3}{2}$��$\frac{3}{2}$��t��2��
��3���֢�BC��ƽ���ı��εı�ʱ�������BC�ij��ȣ��ٸ���ƽ���ı��εĶԱ���������Q�ĺ����꣬Ȼ�����������߽���ʽ������������꣬�Ӷ��ý⣻��BC�ǶԽ���ʱ������ƽ���ı��εĶԽ�����ƽ�������Q�ĺ����꣬Ȼ�����������߽���ʽ������������꣬�Ӷ��ý⣮
��� �⣺��1���ߡ�OAB=90�㣬OB=2����AOB=30�㣬
��AB=1��OA=$\sqrt{3}$��
��B��1��$\sqrt{3}$����
��-$\frac{b}{2a}$=1��$\frac{4a��3a-{b}^{2}}{4a}=\sqrt{3}$��
��ã�a=-$\frac{\sqrt{3}}{4}$��b=$\frac{\sqrt{3}}{2}$��
��y=-$\frac{\sqrt{3}}{4}$x2+$\frac{\sqrt{3}}{2}$x+$\frac{3\sqrt{3}}{4}$��
��y=0���÷���-$\frac{\sqrt{3}}{4}$x2+$\frac{\sqrt{3}}{2}$x+$\frac{3\sqrt{3}}{4}$=0��
���x=3��x=-1
��C��3��0����
��2�����۵����O���ڵ�F����
��0��t��1ʱ���ص�����Ϊ��DEF����ͼ1��ʾ
DE=$\frac{\sqrt{3}}{3}$t��
��S=$\frac{1}{2}$•OD•DE=$\frac{\sqrt{3}}{6}$t2����ʱS�����ֵΪ$\frac{\sqrt{3}}{6}$��
��1��t��$\frac{3}{2}$ʱ���ص�����Ϊ�ı���BDEG����ͼ2��ʾ��
��S=S��DEF-S��BGF
=$\frac{\sqrt{3}}{6}$t2-$\frac{1}{2}$•��2t-2��•$\frac{\sqrt{3}}{2}$��2t-2��
=-$\frac{5\sqrt{3}}{6}$t2+2$\sqrt{3}$t-$\sqrt{3}$
=-$\frac{5\sqrt{3}}{6}$��t-$\frac{6}{5}$��2+$\frac{\sqrt{3}}{5}$
��ʱS�����ֵΪ$\frac{\sqrt{3}}{5}$��
��$\frac{3}{2}$��t��2ʱ���ص�����Ϊ��BDG����ͼ3��ʾ��
��S=$\frac{1}{2}$��2-t��•$\sqrt{3}$��2-t��=$\frac{\sqrt{3}}{2}$��2-t��2
��ʱS�����ֵΪ$\frac{\sqrt{3}}{8}$��
����������S�����ֵΪ$\frac{\sqrt{3}}{5}$��
��3�����ڣ�
��B��1��$\sqrt{3}$����C��3��0��
��BC=$\sqrt{��3-1��^{2}+��\sqrt{3}-0��^{2}}$=$\sqrt{7}$��
��ͼ4��ʾ�����ı���BCPQΪƽ���ı��Σ���BC��PQ��BC=PQ��
���BCM�ա�PQN��
��QN=CM=2��
��Q��-2��-$\frac{5\sqrt{3}}{4}$����
��ͼ5��ʾ�����ı���BCQPΪƽ���ı��Σ���BC��PQ��BC=PQ��
��QN=CM=2��
��Q��2��$\frac{3\sqrt{3}}{4}$����
��ͼ6��ʾ�����ı���BQCPΪƽ���ı��Σ���PB��CQ��PB=CQ��
��BM=CN=1��
��ON=4��
��QN=-$\frac{5\sqrt{3}}{4}$
����������Q1��-2��-$\frac{5\sqrt{3}}{4}$����Q2��2��$\frac{3\sqrt{3}}{4}$����Q3��4��-$\frac{5\sqrt{3}}{4}$����
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ�������ε������ƽ���ı��ζԱ���ȣ��Խ�����ƽ�ֵ����ʣ���������˼������ã�


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 24 | C�� | 36 | D�� | 48 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����5cm | B�� | ����6cm | C�� | ����4cm | D�� | С�ڻ����4cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
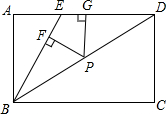 ��ͼ��E�Ǿ���ABCD��AD�ϵ�һ�㣬��BE=ED��P�ǶԽ���BD������һ�㣬PF��BE��F��PG��AD��G���������PF��PG��AB����֮����ʲô��ϵ����֤����Ľ��ۣ�
��ͼ��E�Ǿ���ABCD��AD�ϵ�һ�㣬��BE=ED��P�ǶԽ���BD������һ�㣬PF��BE��F��PG��AD��G���������PF��PG��AB����֮����ʲô��ϵ����֤����Ľ��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
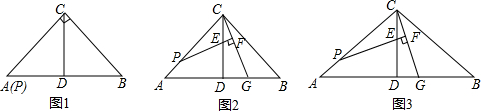
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
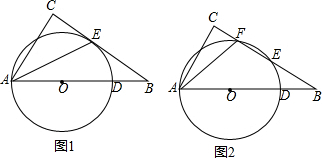
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com