
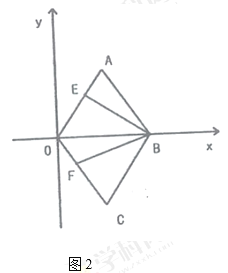
【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.
(1)∠AOC与∠BOD的度数相等吗,为什么?
(2)已知OM平分∠AOC,若射线ON在∠COD的内部,且满足∠AOC与∠MON互余;
①∠AOC=32°,求∠MON的度数;
②试探究∠AON与∠DON之间有怎样的数量关系,请写出结论并说明理由.

【答案】(1)∠AOC=∠BOD,理由详见解析;(2)① 58°;②∠AON=∠DON,理由详见解析.
【解析】
(1)根据补角的性质即可求解;
(2)①根据余角的定义解答即可;
②根据角平分线的定义以及补角与余角的定义,分别用∠AOM的代数式表示出∠AON与∠DON即可解答.
解:(1)∠AOC=∠BOD,
∵∠BOD与∠BOC互补,
∴∠BOD+∠BOC=180°,
∵∠AOC+∠BOC=180°,
∴∠AOC=∠BOD;
(2)①∵∠AOC与∠MON互余,
∴∠MON=90°﹣∠AOC=58°;
②∠AON=∠DON,
理由如下:
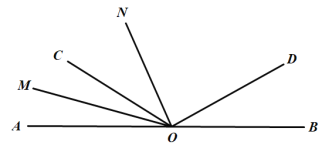
∵OM平分∠AOC,
∴∠AOC=2∠AOM,∠COM=∠AOM,
∵∠AOC与∠MON互余,
∴∠AOC+∠MON=90°,
∴∠AON=90°﹣∠AOM,
∴∠CON=90°﹣3∠AOM,
∵∠BOD与∠BOC互补,
∴∠BOD+∠BOC=180°,
∴∠CON+∠DON+2∠BOD=180°,
又∵∠BOD=∠AOC=2∠AOM,
∴∠DON=180°﹣∠CON﹣2∠BOD
=180°﹣(90°﹣3∠AOM)﹣4∠AOM
=90°﹣∠AOM.
∴∠AON=∠DON.


科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )

A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:对于![]() ,这类不等式我们可以进行下面的解题思路 由有理数的乘法法则两数相乘,同号得正,可得;
,这类不等式我们可以进行下面的解题思路 由有理数的乘法法则两数相乘,同号得正,可得;
![]() 或
或![]() , 从而将陌生的高次不等式化为了学过的一元一次不等式组,分别去解两个不等式组即可求得原不等式组的解集,即: 解不等式组(1)得
, 从而将陌生的高次不等式化为了学过的一元一次不等式组,分别去解两个不等式组即可求得原不等式组的解集,即: 解不等式组(1)得![]() ,解不等式组(2)得
,解不等式组(2)得![]() ,所以
,所以![]() 的解集为
的解集为![]() 或
或![]() .请利用上述解题思想解决下面的问题:
.请利用上述解题思想解决下面的问题:
(1)请直接写出![]() 的解集.
的解集.
(2)对于![]() ,请根据有理数的除法法则化为我们学过的不等式(组).
,请根据有理数的除法法则化为我们学过的不等式(组).
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知图①,在数轴上有一条线段![]() ,点
,点![]() 表示的数分别是
表示的数分别是![]() 和
和![]() .
.
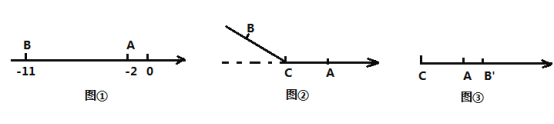
(1)线段![]() ____________;
____________;
(2)若![]() 是线段
是线段![]() 的中点,则点
的中点,则点![]() 在数轴上对应的数为________;
在数轴上对应的数为________;
(3)若![]() 为线段
为线段![]() 上一点.如图②,以点
上一点.如图②,以点![]() 为折点,将此数轴向右对折;如图③,点
为折点,将此数轴向右对折;如图③,点![]() 落在点
落在点![]() 的右边点
的右边点![]() 处,若
处,若![]() ,求点
,求点![]() 在数轴上对应的数是多少?
在数轴上对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
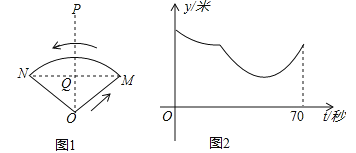
【题目】小阳在如图①所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的点_______(在点P、N、Q、M、O中选取)
查看答案和解析>>
科目:初中数学 来源: 题型:
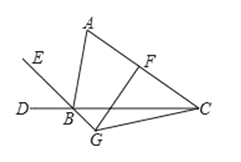
【题目】如图 ,BE平分△ABC的外角∠ABD,F是 AC的中点,过 F点作 AC的垂线交 BE的反向延长线于 G点, 连 EG.若∠ABC=80°,则∠ACG的度数为是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究活动:
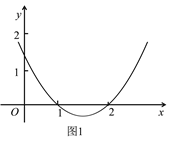
利用函数![]() 的图象(如图1)和性质,探究函数
的图象(如图1)和性质,探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)如图2,小东列表描出了函数![]() 图象上部分点,请画出函数图象;
图象上部分点,请画出函数图象;
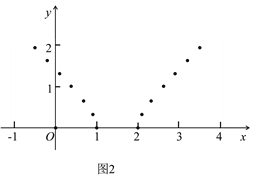
(3)解决问题:设方程![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() ,方程
,方程
![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() .若
.若![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系为_____________________(用“<”连接).
的大小关系为_____________________(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
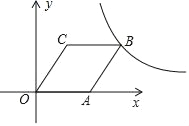
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,![]() ).
).
(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是菱形,
是菱形,![]() ,
,![]()
(1)如图1,作![]() 的平分线
的平分线![]() ,交
,交![]() 于
于![]() (不写作法和证明,保留作图痕迹)
(不写作法和证明,保留作图痕迹)
(2)在(1)的条件下,点![]() 在直线
在直线![]() 上,
上,![]() 最大值时,求
最大值时,求![]() 的长
的长
(3)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点,
上的动点,![]() ,求四边形
,求四边形![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com