
【题目】知图①,在数轴上有一条线段![]() ,点
,点![]() 表示的数分别是
表示的数分别是![]() 和
和![]() .
.
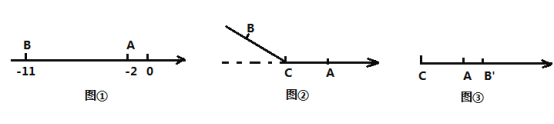
(1)线段![]() ____________;
____________;
(2)若![]() 是线段
是线段![]() 的中点,则点
的中点,则点![]() 在数轴上对应的数为________;
在数轴上对应的数为________;
(3)若![]() 为线段
为线段![]() 上一点.如图②,以点
上一点.如图②,以点![]() 为折点,将此数轴向右对折;如图③,点
为折点,将此数轴向右对折;如图③,点![]() 落在点
落在点![]() 的右边点
的右边点![]() 处,若
处,若![]() ,求点
,求点![]() 在数轴上对应的数是多少?
在数轴上对应的数是多少?
【答案】(1)9;(2)-6.5;(3)-6.
【解析】
(1)根据数轴上两点间的距离公式解决即可;
(2)根据中点的性质,计算即可;
(3)设AB'为x,根据题AB'与B'C的关系,将B'C用x表示出来,然后根据AC、AB、BC的关系,将AB用x表示出来,计算出x的值,即可求出AC的值,然后根据点A的坐标求出点C在数轴上的对应的数即可.
(1)AB的长度为![]() .
.
(2)M是线段AB的中点,所以M点在数轴上对应的点为![]() .
.
(3)设AB'=![]() ,
,
∵AB'=![]() B'C,则B'C=
B'C,则B'C=![]() .
.
∴由题意BC=B'C=![]() ,
,
∴AC=B'C-AB'=![]() ,
,
∴AB=AC+BC=AC+B'C=![]() ,
,
即![]() ,
,
∴![]() ,
,
∴AC=4,
又∵点A表示的数为-2,
∴-2-4=-6,
∴点C表示的数为-6.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=4,D是BC上一个动点,连接AD,以AD为边向右侧作等腰直角△ADE,其中∠ADE=90°.
(1)如图2,G,H分别是边AB,BC的中点,连接DG,AH,EH.求证:△AGD∽△AHE;
(2)如图3,连接BE,直接写出当BD为何值时,△ABE是等腰三角形;
(3)在点D从点B向点C运动过程中,求△ABE周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影“阿凡达”自上映以来取得了空前的票房收入,某小区居民决定通过居委会向影院购买一些3D票供每户家庭观看,最终购得成人票数量是学生(孩子)票数量的3倍,购买的总费 用不低干2200元,但不高于2500元
(1)电影院成人票售价20元/人,学生票售价为50元/人,问:有哪几种购买方案?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)由于当天电影院同时播放“拆弹部队”,故决定成人票打九折,学生票打八折,用(2)中的最少费用最多还可以多买多少张成人票和学生票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 都是格点.
都是格点.
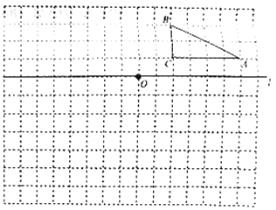
(1)将![]() 向左平移6个单位长度得到
向左平移6个单位长度得到![]() ,请画出
,请画出![]() ;
;
(2)将![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,请画出
,请画出![]() ;
;
(3)作出![]() 关于直线
关于直线![]() 对称的
对称的![]() ,使
,使![]() ,
,![]() ,
,![]() 的对称点分别是
的对称点分别是![]() ,
,![]() ,
,![]() ;
;
(4)![]() 与
与![]() 成______,
成______,![]() 与
与![]() 成______(填“中心对称”或“轴对称”).如果成中心对称请你在图中确定其对称中心点
成______(填“中心对称”或“轴对称”).如果成中心对称请你在图中确定其对称中心点![]() 的位置.
的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,∠E=∠F=90°,∠B=∠C,AC=AB,给出下列结论:① ∠1=∠2;② BE=CF;③ △ACN≌△ABM;④ CD=DN,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.
(1)∠AOC与∠BOD的度数相等吗,为什么?
(2)已知OM平分∠AOC,若射线ON在∠COD的内部,且满足∠AOC与∠MON互余;
①∠AOC=32°,求∠MON的度数;
②试探究∠AON与∠DON之间有怎样的数量关系,请写出结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB =90°,AC = BC =2,AB =![]() ,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.
,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,然后再按笔试占![]() 、面试占
、面试占![]() 计算候选人的综合成绩.他们的各项成绩如下表所示:
计算候选人的综合成绩.他们的各项成绩如下表所示:
候选人 | 笔试成绩/分 | 面试成绩/分 |
甲 |
|
|
乙 |
|
|
丙 |
|
|
丁 |
|
|
(1)现得知候选人丙的综合成绩为![]() 分,求表中
分,求表中![]() 的值
的值
(2)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com