
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=4,D是BC上一个动点,连接AD,以AD为边向右侧作等腰直角△ADE,其中∠ADE=90°.
(1)如图2,G,H分别是边AB,BC的中点,连接DG,AH,EH.求证:△AGD∽△AHE;
(2)如图3,连接BE,直接写出当BD为何值时,△ABE是等腰三角形;
(3)在点D从点B向点C运动过程中,求△ABE周长的最小值.

【答案】(1)证明见解析;(2)当BD=0或![]() 或
或![]() 时,△ABE是等腰三角形.;(3)△ABE周长最小值为
时,△ABE是等腰三角形.;(3)△ABE周长最小值为![]() .
.
【解析】(1)根据等腰直角三角形的性质和相似三角形的判定解答即可;
(2)分三种情况:
①当B与D重合时,即BD=0,如图3,此时AB=BE;
③当AB=AE时,如图4,此时E与C重合,可得BD的长;
③当AB=BE时,如图5,作辅助线,构建等腰直角三角形和全等三角形,证明△ADM≌△DEG,和△EMG是等腰直角三角形,则ME=![]() MG,根据(1)得:△AHD∽△AME,且
MG,根据(1)得:△AHD∽△AME,且![]() ,可计算BD的长;
,可计算BD的长;
(3)先确定△ABE周长的最小值时,E的位置:作点B关于直线MC的对称点N,连接AN交MC于点E′,此时△ABE′就是所求周长最小的△ABE;证明四边形ABMC是正方形,根据△ABD∽△AME,得∠AME=∠ABD=45°,知点E在射线MC上,利用勾股定理求AN的长,根据周长定义可得结论.
(1)证明:如图2,由题意知△ABC和△ADE都是等腰直角三角形,
∴∠B=∠DAE=45°.
∵H为BC中点,
∴AH⊥BC.
∴∠BAH=45°=∠DAE.
∴∠GAD=∠HAE.
在等腰直角△BAH和等腰直角△DAE中,
AH=![]() AB=
AB=![]() AG,AE=
AG,AE=![]() AD.
AD.
∴![]() ,
,
∴△AGD∽△AHE;
(2)解:分三种情况:
①当B与D重合时,即BD=0,如图3,此时AB=BE;
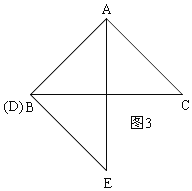
③当AB=AE时,如图4,此时E与C重合,
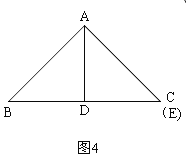
∴D是BC的中点,
∴BD=![]() BC=2
BC=2![]() ;
;
③当AB=BE时,如图5,过E作EH⊥AB于H,交BC于M,连接AM,过E作EG⊥BC于G,连接DH,
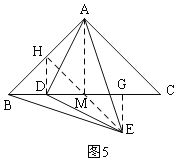
∵AE=BE,EH⊥AB,
∴AH=BH,
∴AM=BM,
∵∠ABC=45°,
∴AM⊥BC,△BMH是等腰直角三角形,
∵AD=DE,∠ADE=90°,
易得△ADM≌△DEG,
∴DM=EG,
∵∠EMG=∠BMH=45°,
∴△EMG是等腰直角三角形,
∴ME=![]() MG,
MG,
由(1)得:△AHD∽△AME,且![]() ,
,
∴∠AHD=∠AME=135°,ME=![]() DH,
DH,
∴∠BHD=45°,MG=DH,
∴△BDH是等腰直角三角形,
∴BD=DH=EG=DM=![]() ;
;
综上所述,当BD=0或![]() 或2
或2![]() 时,△ABE是等腰三角形;
时,△ABE是等腰三角形;
(3)解:当点D与点B重合时,点E的位置记为点M,连接CM,如图6,
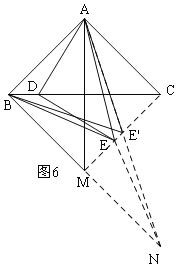
此时,∠ABM=∠BAC=90°,∠AMB=∠BAM=45°,BM=AB=AC.
∴四边形ABMC是正方形.
∴∠BMC=90°,
∴∠AMC=∠BMC-∠AMB=45°,
∵∠BAM=∠DAE=45°,
∴∠BAD=∠MAE,
在等腰直角△BAM和等腰直角△DAE中,
AM=![]() AB,AE=
AB,AE=![]() AD.
AD.
∴![]() .
.
∴△ABD∽△AME.
∴∠AME=∠ABD=45°
∴点E在射线MC上,
作点B关于直线MC的对称点N,连接AN交MC于点E′,
∵BE+AE=NE+AE≥AN=NE′+AE′=BE′+AE′,
∴△ABE′就是所求周长最小的△ABE.
在Rt△ABN中,
∵AB=4,BN=2BM=2AB=8,
∴AN=![]() .
.
∴△ABE周长最小值为AB+AN=4+4![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )

A. 4个 B. 3个
C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )

A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,并解决问题:
我国古代数学的许多发现都曾居世界前列,“杨辉三角”就是其中一例.如图是“杨辉三角”的一部分,其构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和,“杨辉三角”给出了![]() (
(![]() 为正整数)的展开式(按
为正整数)的展开式(按![]() 的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中的系数.
展开式中的系数.

(1)根据上面的规律,直接写出![]() 的展开式共有_______项;
的展开式共有_______项;
(2)直接写出![]() 的展开式;
的展开式;
(3)利用上面的规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
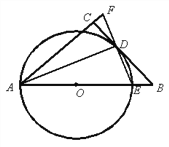
【题目】如图,在△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O与BC相交于点D,与AB交于点E,AD平分∠FAB,连接ED并延长交AC的延长线于点F.
(1)求证:BC为⊙O的切线.
(2)求证:AE=AF;
(3)若DE=3,sin∠BDE=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点![]() 、
、![]() 运动的时间是
运动的时间是![]() 秒
秒![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?若能,求出
能够成为菱形吗?若能,求出![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(3)当![]() ________时,
________时,![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:对于![]() ,这类不等式我们可以进行下面的解题思路 由有理数的乘法法则两数相乘,同号得正,可得;
,这类不等式我们可以进行下面的解题思路 由有理数的乘法法则两数相乘,同号得正,可得;
![]() 或
或![]() , 从而将陌生的高次不等式化为了学过的一元一次不等式组,分别去解两个不等式组即可求得原不等式组的解集,即: 解不等式组(1)得
, 从而将陌生的高次不等式化为了学过的一元一次不等式组,分别去解两个不等式组即可求得原不等式组的解集,即: 解不等式组(1)得![]() ,解不等式组(2)得
,解不等式组(2)得![]() ,所以
,所以![]() 的解集为
的解集为![]() 或
或![]() .请利用上述解题思想解决下面的问题:
.请利用上述解题思想解决下面的问题:
(1)请直接写出![]() 的解集.
的解集.
(2)对于![]() ,请根据有理数的除法法则化为我们学过的不等式(组).
,请根据有理数的除法法则化为我们学过的不等式(组).
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知图①,在数轴上有一条线段![]() ,点
,点![]() 表示的数分别是
表示的数分别是![]() 和
和![]() .
.
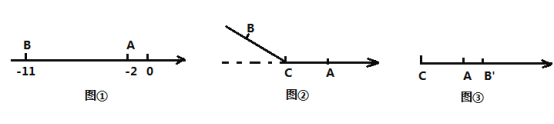
(1)线段![]() ____________;
____________;
(2)若![]() 是线段
是线段![]() 的中点,则点
的中点,则点![]() 在数轴上对应的数为________;
在数轴上对应的数为________;
(3)若![]() 为线段
为线段![]() 上一点.如图②,以点
上一点.如图②,以点![]() 为折点,将此数轴向右对折;如图③,点
为折点,将此数轴向右对折;如图③,点![]() 落在点
落在点![]() 的右边点
的右边点![]() 处,若
处,若![]() ,求点
,求点![]() 在数轴上对应的数是多少?
在数轴上对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
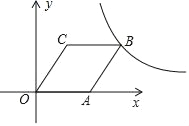
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,![]() ).
).
(1)求图象过点B的反比例函数的解析式;
(2)求图象过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com