Question

【题目】如图，已知反比例函数y=（x＞0）的图象与直线：y=kx+b都经过点P（2，m），Q（n，4），且直线交x轴于点A，交y轴于点B，连接OP，OQ．

（1）直接写出m，n的值；m= , n= ;

（2）求直线的函数表达式；

（3）AP与BQ相等吗？写出你的判断，并说明理由；

Answer 1

【答案】（1）m=1，n=；（2）y=﹣2x+5．（3）相等.

【解析】

（1）反比例函数y=（x＞0）经过点P（2，m），Q（n，4）,把P,Q代入求解;

（2）把P,Q代入y=kx+b求解；

（3）根据直线交x轴于点A，交y轴于点B，求出A,B,再用勾股定理求解.

解：（1）∵反比例函数y=（x＞0）的图象与直线l：y=kx+b都经过点P（2，m），Q（n，4），

∴m=1，n=，…………………………………………2’

（2）∵直线y=kx+b经过点P（2，1），Q（，4），

则有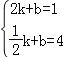，…………………………………………4’

解得，

∴直线l的解析式为y=﹣2x+5．…………………………………………6’

（3）相等．…………………………………………7’

理由：∵y=﹣2x=+5，

∴当y=0时，x=，即OA=，当x=0时，y=5，即OB=5，

∴A，B

∴AP=，

BQ=

∴AP=BQ……（其它方法，酌情赋分）