
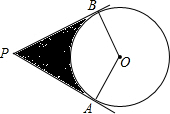
 如图,过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB,切点为A、B,如果∠APB=60°,则图中阴影的面积等于( )
如图,过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB,切点为A、B,如果∠APB=60°,则图中阴影的面积等于( )| A. | 12$\sqrt{3}$-4π | B. | 24$\sqrt{3}$-4π | C. | 12$\sqrt{3}$-2π | D. | 24$\sqrt{3}$-2π |
分析 阴影部分的面积等于四边形OAPB的面积减去扇形AOB的面积.
解答 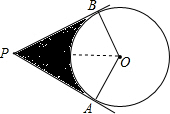 解:连接OP,
解:连接OP,
∵∠APB=60°,
根据切线长定理得∠APO=30°,
∴OP=2OA=4$\sqrt{3}$,AP=OP•cos30°=6,∠AOP=60°,
∴四边形的面积=2S△AOP=2×$\frac{1}{2}$×2$\sqrt{3}$×6=12$\sqrt{3}$;扇形的面积是$\frac{120π×(2\sqrt{3})^{2}}{360}$=4π,
∴阴影部分的面积是12$\sqrt{3}$-4π,
故选A.
点评 本题考查了切线长定理、切线的性质定理以及30°的直角三角形的性质.关键是熟练运用扇形的面积计算公式,能够把四边形的面积转化为三角形的面积计算.


科目:初中数学 来源: 题型:选择题
| A. | 2ab2-2b2 | B. | 2a2b-2b3 | C. | 2a2b+2b2 | D. | 2ab-2ab2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
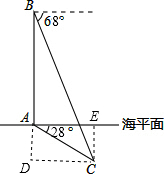 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为27°,测得AC的距离为625米.位于军舰A正上方的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出:
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为27°,测得AC的距离为625米.位于军舰A正上方的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=2 | B. | m≥2 | C. | m<2 | D. | m≤2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com