
分析 根据完全平方公式的变形得到xy=$\frac{1}{2}$,则x4+y4=(x2+y2)2-2x2y2=$\frac{17}{2}$,所以x5+y5=(x+y)[(x4+y4)-xy(x2+y2-xy)],将相关数据代入求值即可.
解答 解:∵2xy=(x+y)2-(x2+y2)=4-3=1,
∴xy=$\frac{1}{2}$,
∴x4+y4=(x2+y2)2-2x2y2=32-2×($\frac{1}{2}$)2=$\frac{17}{2}$,
∴x5+y5
=(x+y)(x4-x3y+x2y2-xy3+y4)
=(x+y)(x4+y4-x3y+x2y2-xy3)
=(x+y)[(x4+y4)-xy(x2+y2-xy)]
=2×[$\frac{17}{2}$-$\frac{1}{2}$(3-$\frac{1}{2}$)]
=14.5.
故答案是:14.5.
点评 本题考查了完全平方公式.熟记公式结构是解题的关键.完全平方公式(a+b)2=a2+2ab+b2的变形公式有:a2+b2=(a+b)2-2ab,2ab=(a+b)2-a2+b2.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
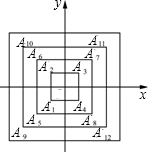 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )| A. | (13,13) | B. | (-13,-13) | C. | (-14,-14) | D. | (14,14) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=4x+3 | B. | y=4x-3 | C. | y=4(x+3) | D. | y=4(x-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com