
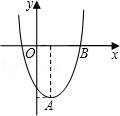
【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)(4,0).
【解析】
试题分析:(1)有顶点就用顶点式来求二次函数的解析式;
(2)由于是向右平移,可让二次函数的y的值为0,得到相应的两个x值,算出负值相对于原点的距离,而后让较大的值也加上距离即可.
试题解析:(1)∵二次函数图象的顶点为A(1,﹣4),
∴设二次函数解析式为y=a(x﹣1)2﹣4,
把点B(3,0)代入二次函数解析式,得:
0=4a﹣4,解得a=1,
∴二次函数解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)令y=0,得x2﹣2x﹣3=0,解方程,得x1=3,x2=﹣1.
∴二次函数图象与x轴的两个交点坐标分别为(3,0)和(﹣1,0),
∴二次函数图象上的点(﹣1,0)向右平移1个单位后经过坐标原点.
故平移后所得图象与x轴的另一个交点坐标为(4,0).


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的A1处,则∠A、∠1、∠2之间满足的关系式是( )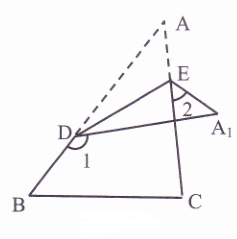
A.∠A=∠1-∠2
B.∠A= ![]() ∠1-∠2
∠1-∠2
C.∠A=∠1-2∠2
D.2∠A=∠1-∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
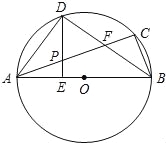
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,AB=5,射线AX垂直于AC,点A为垂足,一条长度为5的线段PQ的两个端点P、Q分别在边AC和射线AX上运动,则当AP=___________ 时,ΔABC与ΔPQA全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动: ①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书超过200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com