
分析 等式整理后,不能求出a,b,c的值,所以考虑将变形等式.把b-c变形为(a-c)+(b-a),两边都除以(a-b),得到$\frac{c-a}{a-b}$的值,把要求的分式变形,使变形后的分式只含有$\frac{c-a}{a-b}$,再整体代入.
解答 解:5(a-b)+$\sqrt{5}$(b-c)+(c-a)=0,
5(a-b)+$\sqrt{5}$[(a-c)+(b-a)]+(c-a)=0,
5(a-b)+$\sqrt{5}$(a-c)+$\sqrt{5}$(b-a)+(c-a)=0,
等式两边都除以(a-b)得,
5-$\frac{\sqrt{5}(c-a)}{a-b}-\sqrt{5}+\frac{c-a}{a-b}$=0
(1-$\sqrt{5}$)$\frac{c-a}{a-b}$=$\sqrt{5}$-5
整理,得$\frac{c-a}{a-b}$=$\sqrt{5}$
$\frac{(c-b)(c-a)}{(a-b)^{2}}$
=$\frac{c-b}{a-b}×\frac{c-a}{a-b}$
=$\frac{(a-b)+(c-a)}{a-b}$×$\sqrt{5}$
=[$\frac{a-b}{a-b}+\frac{c-a}{a-b}$]×$\sqrt{5}$
=(1+$\sqrt{5}$)×$\sqrt{5}$
=$\sqrt{5}+5$.
点评 本题考查了等式及分式的化简变形,求出$\frac{c-a}{a-b}$的值变形分式的值整体代入是关键.


科目:初中数学 来源: 题型:填空题
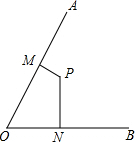 如图,∠AOB=60°,点P在∠AOB的内部,且点P到OA、OB的距离为a和b,且a<b,点M在OA上,点N在OB上,则PM+MN的最小值为a+b.
如图,∠AOB=60°,点P在∠AOB的内部,且点P到OA、OB的距离为a和b,且a<b,点M在OA上,点N在OB上,则PM+MN的最小值为a+b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
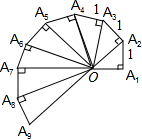 如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.
如图是第七届国际数学教育大会的会徽示意图,主题图案是由一连串如图所示的直角三角形演化而成的.其中的第一个三角形OA1A2是等腰直角三角形,且OA1=A1A2=A2A3…=A8A9=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为 ________________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 意见 | 频数 | 频率 |
| 赞同 | $\frac{1}{6}$ | |
| 不赞同 | 19 | $\frac{1}{6}$ |
| 不能确定 | 3 | 0.06 |
| 总计 | 50 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com