
【题目】已知:在△ABC中,D为BC边上一点,B,C两点到直线AD的距离相等.
(1)如图1,若△ABC是等腰三角形,AB=AC,则点D的位置在;
(2)如图2,若△ABC是任意一个锐角三角形,猜想点D的位置是否发生变化,请补全图形并加以证明;
(3)如图3,当△ABC是直角三角形,∠A=90°,并且点D满足(2)的位置条件,用等式表示线段AB,AC,AD之间的数量关系并加以证明.
【答案】
(1)点D为线段BC的中点
(2)证明:如图1,作BE⊥AD于点E,CF⊥AD于点F,

∵BE⊥AD于点E,CF⊥AD于点F,
∴∠3=∠4=90°,
在△BED和△CFD中,
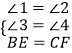
∴△BED≌△CFD.
∴BD=DC.即点D是BC边的中点.
(3)证明:如图2,延长AD到点H使DH=AD,连接HC.
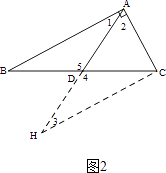
∵点D是BC边的中点,
∴BD=DC.
在△ABD和△HCD中,

∴△ABD≌△HCD.
∴∠1=∠3,AB=CH.
∵∠A=90°,
∴∠1+∠2=90°.
∴∠2+∠3=90°.
∴∠ACH=90°.
∴AC2+CH2=AH2.
又∵DH=AD,
∴AC2+AB2=(2AD)2.
∴AC2+AB2=4AD2.
【解析】(1)根据等腰三角形底边上的三线合一知D点在BC的中点处;
(2)作BE⊥AD于点E,CF⊥AD于点F,根据垂直的定义得出∠3=∠4=90°,然后利用AAS判断出△BED≌△CFD.根据全等三角形对应边相等得出BD=DC.即点D是BC边的中点;
(3)延长AD到点H使DH=AD,连接HC.根据中点定义得BD=DC,然后由SAS判断出△ABD≌△HCD,根据全等三角形的性质得∠1=∠3,AB=CH.然后根据等量代换得出∠ACH=90°.根据够勾股定理得出AC2+CH2=AH2.又因DH=AD,故AC2+AB2=(2AD)2,即AC2+AB2=4AD2.


科目:初中数学 来源: 题型:
【题目】在彩虹读书活动中,某校决定为八年级学生购买同等数量的《钢铁是怎样炼成的》和《居里夫人自传》,供学生借阅.其中《居里夫人自传》的单价比《钢铁是怎样炼成的》的单价多8元.若学校购买《居里夫人自传》用了1 000元,购买《钢铁是怎样炼成的》用了600元,请问两种书的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家最近新盖了房子,室内装修时,木工师傅让小红爸爸去建材市场买一块长3m,宽2.2m的薄木板用来做家居面,到了市场爸爸看到满足这个尺寸的木板有点大,买还是不买爸爸犹豫了,因为他知道他家门框高只有2m,宽只有1m,他不知道这块木板买回家后能不能完整的通过自家门框.请你替小红爸爸解决一下难题,帮他算一算要买的木板能否通过自家门框进入室内.(备用图可供做题参考,薄木板厚度可以忽略不计)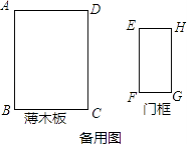
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,连接OC,OB,则图中全等的三角形有( )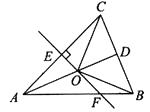
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,
(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com