
【题目】如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2 , 以OA2为直角边作等腰Rt△OA2A3 , …则OA5的长度为 . 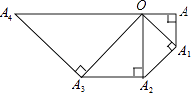
【答案】4 ![]()
【解析】解:∵△OAA1为等腰直角三角形,OA=1, ∴AA1=OA=1,OA1= ![]() OA=
OA= ![]() ;
;
∵△OA1A2为等腰直角三角形,
∴A1A2=OA1= ![]() ,OA2=
,OA2= ![]() OA1=2;
OA1=2;
∵△OA2A3为等腰直角三角形,
∴A2A3=OA2=2,OA3= ![]() OA2=2
OA2=2 ![]() ;
;
∵△OA3A4为等腰直角三角形,
∴A3A4=OA3=2 ![]() ,OA4=
,OA4= ![]() OA3=4.
OA3=4.
∵△OA4A5为等腰直角三角形,
∴A4A5=OA4=4,OA5= ![]() OA4=4
OA4=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. 请解决下列问题: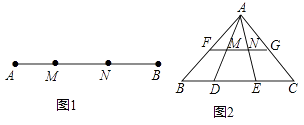
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有3个形状大小完全一样的小球,上面分别有标号1,2,-1,用树状图或列表的方法解决下列问题:
(1)将球搅匀,从盒中一次取出两个球,求其两标号互为相反数的概率。
(2)将球搅匀,摸出一个球将其标号记为k,放回后搅匀后再摸出一个球,将其标号记为b.求直线y=kx+b不经过第三象限的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com