
【题目】如图1,在平面直角坐标系xOy中,抛物线y=-(x-a)(x-4)(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
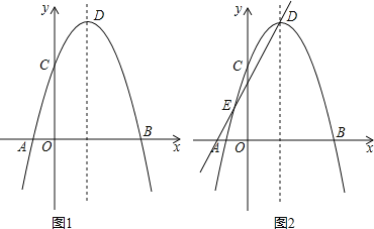
(1)若D点坐标为(![]() ),求抛物线的解析式和点C的坐标;
),求抛物线的解析式和点C的坐标;
(2)若点M为抛物线对称轴上一点,且点M的纵坐标为a,点N为抛物线在x轴上方一点,若以C、B、M、N为顶点的四边形为平行四边形时,求a的值;
(3)直线y=2x+b与(1)中的抛物线交于点D、E(如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为D′,与直线的另一个交点为E′,与x轴的交点为B′,在平移的过程中,求D′E′的长度;当∠E′D′B′=90°时,求点B′的坐标.
【答案】(1)y=-x2+3x+4,C(0,4);(2)a1=-2-2![]() ,a2=
,a2=![]() ;(3)D′E′=2
;(3)D′E′=2![]() ,B′(-1,0).
,B′(-1,0).
【解析】
(1)将点D的坐标代入函数解析式,求得a的值;利用抛物线解析式来求点C的值.
(2)需要分类讨论:BC为边和BC为对角线两种情况,根据“平行四边形的对边平行且相等,平行四边形的对角线相互平分”的性质列出方程组,利用方程思想解答.
(3)根据平移规律得到D′E′的长度、平移后抛物线的解析式,然后由函数图象上点的坐标特征求得点B′的坐标.
(1)依题意得:![]() =-(
=-(![]() -a)(
-a)(![]() -4).
-4).
解得a=-1.
∴抛物线解析式为:y=-(x+1)(x-4)或y=-x2+3x+4.
∴C(0,4).
(2)由题意知:A(a,0),B(4,0),C(0,-4a).
对称轴为直线x=![]() ,则M(
,则M(![]() ,a).
,a).
①MN∥BC且MN=BC,根据点的平移特征可知N(![]() ,-3a).
,-3a).
则-3a=-(![]() -a)(
-a)(![]() -4).
-4).
解得:a=-2±2![]() (舍去正值).
(舍去正值).
②当BC为对角线时,设N(x,y).
根据平行四边形的对角线互相平分可得: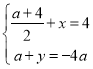 .
.
解得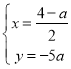 .
.
则-5a=-(![]() -a)(
-a)(![]() -4).
-4).
解得a=![]() .(舍去正值)
.(舍去正值)
∴a1=-2-2![]() ,a2=
,a2=![]() .
.
(3)把D(![]() )代入y=2x+b得到:2×
)代入y=2x+b得到:2×![]() +b=
+b=![]() .则b=
.则b=![]() .
.
故直线解析式为:y=2x+![]() .
.
联立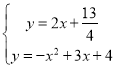 .
.
解得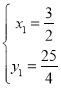 (舍去),
(舍去),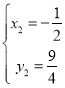 .
.
∴E(-![]() ,
,![]() )
)
∴DE=2![]() .
.
根据抛物线的平移规律,则平移后线段D′E′始终等于2![]() .
.
设平移后的D′(m,2m+![]() ),则E′(m-2,2m-
),则E′(m-2,2m-![]() ).
).
平移后抛物线的解析式为:y=-(x-m)2+2m+![]() .
.
则D′B′:y=-![]() x+n过点(m,2m+
x+n过点(m,2m+![]() ),
),
∴y=-![]() x+
x+![]() m+
m+![]() ,则B′(5m+
,则B′(5m+![]() ,0).
,0).
∴-![]() (5m+
(5m+![]() )+
)+![]() m+
m+![]() =0.
=0.
解得m1=-![]() ,m2=-
,m2=-![]() .
.
∴B′1(-1,0),B′2(-![]() ,0)(与D′重合,舍去).
,0)(与D′重合,舍去).
综上所述,B′(-1,0).


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
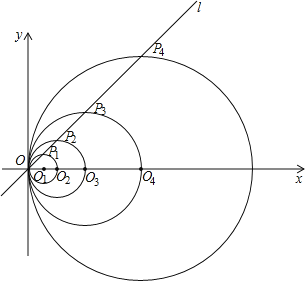
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长_____
的长_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民用水情况,小明在某小区随机抽查了20户家庭的月用水量,结果如下表:
月用水量(m3) | 4 | 5 | 6 | 8 | 9 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6m![]() B.平均数是5.8m
B.平均数是5.8m![]()
C.众数是6m![]() D.极差是6m
D.极差是6m![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】可以用如下方法求方程x2-2x-2=0的实数根的范围:利用函数y=x2-2x-2的图象可知,当x=0时,y<0,当x=-1时,y>0,所以方程有一个根在-1和0之间.
(1)参考上面的方法,求方程x2-2x-2=0的另一个根在哪两个连续整数之间;
(2)若方程x2-2x+c=0有一个根在0和1之间,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.


(1)求证:BG=DG;
(2)求C′G的长;
(3)如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成,图中,第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成,…,那么组成第8个黑色L形的正方形个数为( )

A.31B.20C.37D.33
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com