
分析 先求得反比例函数的解析式,再求得B点坐标,最后由平移后的一次函数图象得到与x轴的交点坐标.
解答 解:∵反比例函数y=$\frac{k}{x}$的图象经过点(4,1),
∴k=4×1=4,
∴反比例函数解析式为y=$\frac{4}{x}$,
把B(1,m)代入反比例函数解析式,可得m=4,
∴B(1,4),
设一次函数y=x+1的图象平移后得到y=x+b,
把B(1,4)代入,可得4=1+b,
解得b=3,
∴平移后的一次函数为y=x+3,
当y=0时,x=-3,
∴平移后的一次函数图象与x轴的交点坐标为(-3,0).
点评 本题主要考查了反比例函数图象上点的坐标特征以及一次函数图象平移的规律的运用,解题时注意:当k的值相等时,两直线可由平移相互得到;一次函数图象与x轴的交点的纵坐标为0.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
在?ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
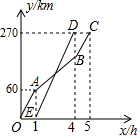 小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
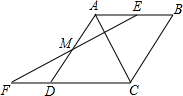 如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
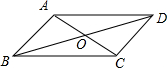 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
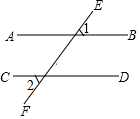 如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )
如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )| A. | ∠2=35° | B. | ∠2=45° | C. | ∠2=55° | D. | ∠2=125° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com