
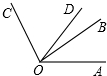
 如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=25°,求∠AOB的度数.
如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=25°,求∠AOB的度数. 科目:初中数学 来源: 题型:解答题
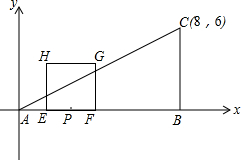 在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.
在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
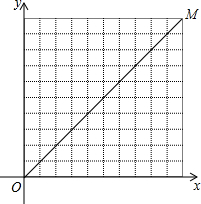 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )| A. | 7 | B. | 8 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com