
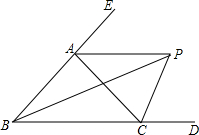
 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P.| 2α+∠BAC |
| 2 |
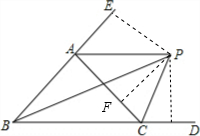 解:(1)如图,过点P作PD⊥BD、PE⊥BE、PF⊥AC;
解:(1)如图,过点P作PD⊥BD、PE⊥BE、PF⊥AC;| 2α+∠BAC |
| 2 |
| 180°-80° |
| 2 |


科目:初中数学 来源: 题型:
 某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com