
分析 所求方程组变形后,根据已知方程组的解求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{\frac{5}{7}{a}_{1}x+\frac{6}{7}{b}_{1}y={c}_{1}}\\{\frac{5}{7}{a}_{2}x+\frac{6}{7}{b}_{2}y={c}_{2}}\end{array}\right.$,
由方程组$\left\{\begin{array}{l}{a_1}x+{b_1}y={c_1}\\{a_2}x+{b_2}y={c_2}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,得到$\left\{\begin{array}{l}{\frac{5}{7}x=-1}\\{\frac{6}{7}y=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{7}{5}}\\{y=-\frac{7}{3}}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=-\frac{7}{5}}\\{y=-\frac{7}{3}}\end{array}\right.$
点评 此题考查了二元一次方程的解,利用了类比的思想,弄清已知方程组解的特征是解本题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
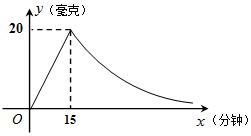 为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
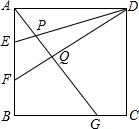 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com