

分析 (1)根据题意即可得到结论;
(2)当P、Q两点相遇时,P、Q表示的数相等列方程得到t=2,于是得到当t=2时,P、Q相遇,即可得到结论;
(3)由t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,于是得到PQ=|(-2+3t)-(8-2t)|=|5t-10|,列方程即可得到结论;
(4)由点M表示的数为 $\frac{-2+(-2+3t)}{2}$=$\frac{3t}{2}$-2,点N表示的数为 $\frac{8+(-2+3t)}{2}$=$\frac{3t}{2}$+3,即可得到结论.
解答 解:(1)①10,3;
②-2+3t,8-2t;
(2)∵当P、Q两点相遇时,P、Q表示的数相等
∴-2+3t=8-2t,
解得:t=2,
∴当t=2时,P、Q相遇,
此时,-2+3t=-2+3×2=4,
∴相遇点表示的数为4;
(3)∵t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,
∴PQ=|(-2+3t)-(8-2t)|=|5t-10|,
又PQ=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5,
∴|5t-10|=5,
解得:t=1或3,
∴当:t=1或3时,PQ=$\frac{1}{2}$AB;
(4)∵点M表示的数为 $\frac{-2+(-2+3t)}{2}$=$\frac{3t}{2}$-2,
点N表示的数为 $\frac{8+(-2+3t)}{2}$=$\frac{3t}{2}$+3,
∴MN=|($\frac{3t}{2}$-2)-($\frac{3t}{2}$+3)|=|$\frac{3t}{2}$-2-$\frac{3t}{2}$-3|=5.
点评 本题考查了一元一次方程的应用应用和数轴,解题的关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


科目:初中数学 来源: 题型:选择题
| A. | ①②均用代入法 | B. | ①②均用加减法 | ||
| C. | ①用代入法,②用加减法 | D. | ①用加减法,②用代入法 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.
如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
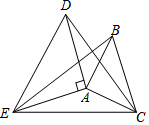 如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )| A. | ①③ | B. | ②④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com