

���� ��1����C��CD��AB��D�����ݵ���ֱ�������ε����ʵõ���ABC=��BAC=45�㣬�õ���KBC=30�㣬����ֱ�������ε����ʵõ�BC=4$\sqrt{3}$�����CD=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{6}$����ֱ�������μ��ɵõ����ۣ�
��2����ͼ2������DF��CD�����ݵ���ֱ�������ε����ʵõ�CD=BD����CDB=90�㣬��ȫ�������ε����ʵõ�BE=CF��CE=AF���Ƴ���BDE�ա�CDF������ȫ�������ε����ʵõ���EDB=��FDC��DE=DF��������ǵ����ʵõ���EDF=90�㣬���ݵ���ֱ�������ε����ʵõ�EF=$\sqrt{2}$DE�����ǵõ����ۣ�
��3��BE+AF=$\sqrt{2}$DE������CD��DF���ɣ�2��֤�á�BCE�ա�ACF������ȫ�������ε����ʵõ�BE=CF��CE=AF���ɣ�2��֤�á�DEF�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ�EF=$\sqrt{2}$DE�����ɵõ����ۣ�
���  �⣺��1����C��CD��AB��D��
�⣺��1����C��CD��AB��D��
��AC=BC����ACB=90�㣬
���ABC=��BAC=45�㣬
�ߡ�MBN=15�㣬
���KBC=30�㣬
��BK=8��
��BC=4$\sqrt{3}$��
��CD=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{6}$��
�ߡ�MCA=15�㣬��BAC=45�㣬
���M=30�㣬
��CM=2CD=4$\sqrt{6}$��
��2����BE��CE��
���BEC=��ACB=90�㣬
���EBC+��BCE=��BCE+��ACF=90�㣬
���EBC=��CAF��
��AF��l�ڵ�F��
���AFC=90�㣬
�ڡ�BCE���ACF�У�$\left\{\begin{array}{l}{��AFC=��BEC=90��}\\{��EBC=��ACF}\\{BC=AC}\end{array}\right.$��
���ACF�ա�CBE��
��ͼ2������DF��CD��
�ߵ�D��AB���е㣬
��CD=BD����CDB=90�㣬
�ߡ�ACF�ա�CBE��
��BE=CF��CE=AF��
�ߡ�EBD=��DCF��
�ڡ�BDE���CDF�У�
$\left\{\begin{array}{l}{BE=CF}\\{��EBD=��FCD}\\{BD=CF}\end{array}\right.$��
���BDE�ա�CDF��
���EDB=��FDC��DE=DF��
�ߡ�CDF+��FDB=90�㣬��EDB+��BDF=90�㣬
���EDF=90�㣬
���EDF�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$DE��
��AF=CE=EF+CF=BE+$\sqrt{2}$DE��
��3����ͼ3������CD��DF��
�ɣ�2��֤�á�BCE�ա�ACF��
��BE=CF��CE=AF��
�ɣ�2��֤�á�DEF�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$DE��
��EF=CE+CF=AF+BE=$\sqrt{2}$DE��
��AF+BE=$\sqrt{2}$DE��
���� ���⿼����ȫ�������ε��ж������ʣ�����ֱ�������ε��ж������ʣ�ֱ��������б���ϵ����ߵ���б�߳���һ�룬֤�á�BCE�ա�ACF�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ھ��ô��뷨 | B�� | �٢ھ��üӼ��� | ||
| C�� | ���ô��뷨�����üӼ��� | D�� | ���üӼ��������ô��뷨 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
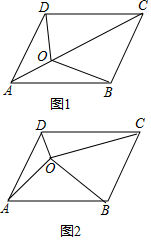 ����֪��ƽ���ı��ε������Խ��߰�ƽ���ı��ηֳ����ĸ������ȵ�С�����Σ�
����֪��ƽ���ı��ε������Խ��߰�ƽ���ı��ηֳ����ĸ������ȵ�С�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com