Question

如图1，在Rt△ABC中，∠C=90º，AC=4cm，BC=3cm，点P由点B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由点A出发沿AC方向向点C匀速运动，速度为2cm/s；连结PQ。若设运动时间为t（s）（0<t<2)，解答下列问题：

（1）当t为何值时？PQ//BC？

（2）设△APQ的面积为y（cm2），求y与t之间的函数关系？

（3）是否存在某一时刻t，使线段PQ恰好把△ABC的周长和面积同时平分？若存在求出此时t的值；若不存在，说明理由。

（4）如图2，连结PC，并把△PQC沿AC翻折，得到四边形PQP'C，那么是否存在某一时刻t，使四边形PQP'C为菱形？若存在求出此时t的值；若不存在，说明理由。

 

Answer 1

【解析】

试题分析：（1）当PQ∥BC时，我们可得出三角形APQ和三角形ABC相似，那么可得出关于AP，AB，AQ，AC的比例关系，我们观察这四条线段，已知的有AC，根据P，Q的速度，可以用时间t表示出AQ，BP的长，而AB可以用勾股定理求出，这样也就可以表示出AP，那么将这些数值代入比例关系式中，即可得出t的值．

（2）求三角形APQ的面积就要先确定底边和高的值，底边AQ可以根据Q的速度和时间t表示出来．关键是高，可以用AP和∠A的正弦值来求．AP的长可以用AB-BP求得，而sinA就是BC：AB的值，因此表示出AQ和AQ边上的高后，就可以得出y与t的函数关系式．

（3）如果将三角形ABC的周长和面积平分，那么AP+AQ=BP+BC+CQ，那么可以用t表示出CQ，AQ，AP，BP的长，那么可以求出此时t的值，我们可将t的值代入（2）的面积与t的关系式中，求出此时面积是多少，然后看看面积是否是三角形ABC面积的一半，从而判断出是否存在这一时刻．

（4）过点P作PM⊥AC于M，PN⊥BC于N，那么PNCM就是个矩形，解题思路：通过三角形BPN和三角形ABC相似，得出关于BP，PN，AB，AC的比例关系，即可用t表示出PN的长，也就表示出了MC的长，要想使四边形PQP'C是菱形，PQ=PC，根据等腰三角形三线合一的特点，QM=MC，这样有用t表示出的AQ，QM，MC三条线段和AC的长，就可以根据AC=AQ+QM+MC来求出t的值．求出了t就可以得出QM，CM和PM的长，也就能求出菱形的边长了．

试题解析：(1) 连接PQ，

若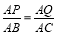时，PQ//BC，即，

∴ t=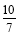

(2) 过P作PD⊥AC于点D，则有，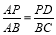

即，

∴ PD=

∴ y==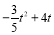（0<t<2)

(3) 若平分周长则有：

AP+AQ=(AB+AC+BC),

即：5－t+2t=6，

∴ t=1

当t=1时，y=3.4；而三角形ABC的面积为6，显然不存在。

过P作PD⊥AC于点D，若QD=CD，则PQ=PC，四边形PQP'C就为菱形。

同(2)方法可求AD=，所以：

-2t=4-；

解之得：t=。

即t=时，四边形PQP'C为菱形。

考点: 相似形综合题.