
分析 (1)直接化简二次根式进而求出答案;
(2)直接利用绝对值的性质化简进而求出答案;
(3)直接利用幂的乘方运算法则以及同底数幂的乘除法运算法则求出答案;
(4)直接利用积的乘方运算法则以及同底数幂的乘法运算法则求出答案;
(5)直接去括号,再合并同类项求出答案;
(6)直接利用完全平方公式去括号,进而合并同类项求出答案.
解答 解:(1)$\frac{1}{3}$×$\sqrt{0.36}$+$\frac{1}{5}$×$\sqrt{900}$-($\sqrt{1+\frac{9}{16}}$-$\sqrt{2.25}$)$\frac{1}{3}$
=0.2+6-($\frac{5}{4}$-1.5)×$\frac{1}{3}$
=6$\frac{17}{60}$;
(2)|1-$\sqrt{2}$|+|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{3}$-2|
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$
=1;
(3)x2•(x2)3÷x5
=x2•x6÷x5
=x3;
(4)-3xy2z•(x2y)2
=-3xy2z•x4y2
=-3x5y4z;
(5)x(x2-1)+2x2(x+1)-3x(2x-5)
=x3-x+2x3+2x2-6x2+15x
=3x3-4x2+14x;
(6)(a+b)2-(a-b)2
=a2+2ab+b2-(a2-2ab+b2)
=4ab.
点评 此题主要考查了整式的混合运算以及积的乘方运算法则和幂的乘方运算等知识,熟练掌握运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
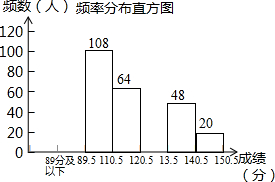 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:| 分组 | 频数 | 频率 |
| 89分及以下 | ||
| 89.5-110.5 | 108 | |
| 110.5-120.5 | 64 | 0.16 |
| 120.5-130.5 | 0.20 | |
| 130.5-140.5 | 48 | |
| 140.5-150.5 | 20 | 0.05 |
| 合计 | 400 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com