
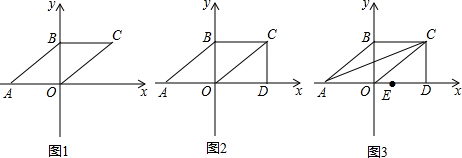
分析 (1)根据平移的性质即可得到结论;
(2)根据CD⊥x轴于点D,于是得到CD=3,即h=3,OD=4,求得DE=3,于是得到结论;
(3)①设P1(1,y),根据S△ACP=S四边形PEDC+S△AEP-S△ADC=$\frac{3(3+y)}{2}+\frac{5y}{2}-\frac{8×3}{2}$=$\frac{33}{2}$,求得y=6,得到P1(1,6)
②设P2(1,-a),如图3,过P作PL∥AD交CD的延长线于L,过A作AH⊥PL于H,根据S△ACP=S四边形AHLC-S△AHP-S△LCP=$\frac{8(2a+3)}{2}-\frac{5a}{2}-\frac{3(a+3)}{2}$=$\frac{33}{2}$,求得a=$\frac{9}{4}$得到P2(1,-$\frac{9}{4}$).
解答 解:(1)∵B(0,3),将AB向右平移4个单位长度至OC的位置,
∴C(4,3),
故答案为:(4,3);
(2)∵CD⊥x轴于点D,
∴CD=3,即h=3,OD=4,
∵E(1,0),
∴DE=3,
∴S△PCD=$\frac{1}{2}$×3×3=$\frac{9}{2}$;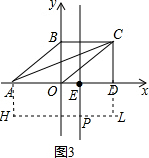 (3)①设P1(1,y),
(3)①设P1(1,y),
∴S△ACP=S四边形PEDC+S△AEP-S△ADC
=$\frac{3(3+y)}{2}+\frac{5y}{2}-\frac{8×3}{2}$=$\frac{33}{2}$,
∴y=6,
∴P1(1,6)
②设P2(1,-a),如图3,过P作PL∥AD交CD的延长线于L,过A作AH⊥PL于H,
∴S△ACP=S四边形AHLC-S△AHP-S△LCP
=$\frac{8(2a+3)}{2}-\frac{5a}{2}-\frac{3(a+3)}{2}$=$\frac{33}{2}$,
∴a=$\frac{9}{4}$
∴P2(1,-$\frac{9}{4}$),
综上所述:P(1,6),(1,-$\frac{9}{4}$).
点评 本题考查了坐标与图形的性质,三角形的面积的计算,图形的变换-平移,正确的识别图形是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x2-x+1=x(2x-1)+1 | B. | x2-2x-1=(x2-1)2 | ||
| C. | 2x2-xy-x=2x(x-y-1) | D. | x2-x-6=(x+2)(x-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
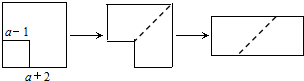
| A. | 4a+1 | B. | 4a+3 | C. | 6a+3 | D. | a2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
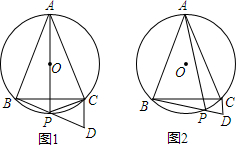
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| (人/只) | 5 | 3 |
| (元/只) | 160 | 105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com