
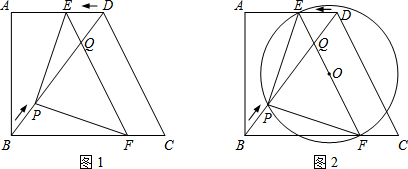
���� ��1���ɹ��ɶ������BD����PE��ABʱ����PEA=��DEP=90�㣬��PK��AB��K����PK=AE��PK��AD����$\frac{PK}{AD}=\frac{BP}{BD}$���ó�AE=PK=$\frac{3}{5}$t����AD=AE+ED=$\frac{3t}{5}$+t=9���ⷽ�̼��ɣ�
��2������P��BC��ƽ���ߣ���EF��G����BD=15=BC���ó���BCD=��BDC����ƽ���ߵ����ʵó�֤����DEQ=��EQD���ó�DQ=DE=t��ͬ����PG=PQ=15-2t���ó�S=$\frac{1}{2}$PG•AB�����ɵó������
��3������P��BC�Ĵ��ߣ���AD��M����BC��N�����PME=��FNP=90�㣬����PEF�����ԲԲ��Oǡ����EF���е㣬��EFΪֱ������Բ�ܽǶ����ó���EPF=90�㣬֤����PEM=��FPN���ó���EMP�ס�PNF���ó���Ӧ�߳ɱ���$\frac{EM}{MP}$=$\frac{PN}{NF}$���������t��ֵ��
��� �⣺��1���ߡ�A=90��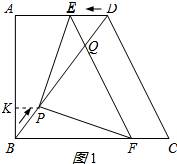
��BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{1{2}^{2}+{9}^{2}}$=15��
��PE��ABʱ����PEA=��DEP=90�㣬
��PK��AB��K����ͼ1��ʾ��
��PK=AE��PK��AD��
��$\frac{PK}{AD}=\frac{BP}{BD}$����$\frac{PK}{9}=\frac{t}{15}$��
��AE=PK=$\frac{3}{5}$t��
��AD=AE+ED=$\frac{3t}{5}$+t=9��
��ã�t=$\frac{45}{8}$��
��2������P��BC��ƽ���ߣ���EF��G����ͼ2��ʾ��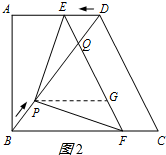
��BD=15=BC��
���BCD=��BDC��
��AD��BC��EF��DC��
��ϡ�DEQ=��BCD����EQD=��BDC��
���DEQ=��EQD��
��DQ=DE=t��
ͬ����PG=PQ=15-2t��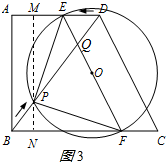
��S=$\frac{1}{2}$PG•AB=$\frac{1}{2}$��12��15-2t��=90-12t
��3������P��BC�Ĵ��ߣ���AD��M����BC��N����ͼ3��ʾ��
���PME=��FNP=90�㣬
���MPE+��PEM=90�㣬
����PEF�����ԲԲ��Oǡ����EF���е㣬
��EFΪֱ����
���EPF=90�㣬
���MPE+��FPN=90�㣬
���PEM=��FPN��
���EMP�ס�PNF��
��$\frac{EM}{MP}$=$\frac{PN}{NF}$����$\frac{9-\frac{8}{5}t}{12-\frac{4}{5}t}=\frac{\frac{4}{5}t}{15-\frac{8}{5}t}$��
��ã�t=$\frac{15}{4}$��$\frac{45}{4}$��
��2t��15��
��t��$\frac{15}{2}$��
��t=$\frac{15}{4}$��
���� ������Բ���ۺ���Ŀ��������ֱ�����ε����ʡ����������ε��ж������ʡ�Բ�ܽǶ��������������ε��ж������ʡ�ƽ���ߵ����ʵ�֪ʶ�������ۺ���ǿ����һ���Ѷȣ��ر��ǣ�3���У���Ҫͨ����������֤�����������ƺ�����Բ�ܽǶ������ܵó������


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
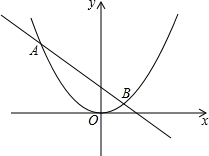 ��֪������y=$\frac{1}{4}$x2��ֱ��y=$-\frac{3}{4}$x+1����A��B���㣨A��B����ࣩ
��֪������y=$\frac{1}{4}$x2��ֱ��y=$-\frac{3}{4}$x+1����A��B���㣨A��B����ࣩ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
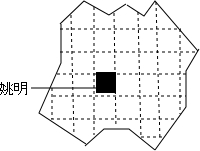 ij��װ��˾����һ�Ų�����İ�װֽ��һ��������ֽ�У���ͼ��
ij��װ��˾����һ�Ų�����İ�װֽ��һ��������ֽ�У���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
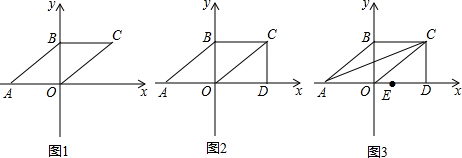
 ��ͼ���ڡ�ABC�У�AB=AC���ӳ�AB��D��ʹBD=AB��EΪAB���е㣬����CE��CD����֤��
��ͼ���ڡ�ABC�У�AB=AC���ӳ�AB��D��ʹBD=AB��EΪAB���е㣬����CE��CD����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com