
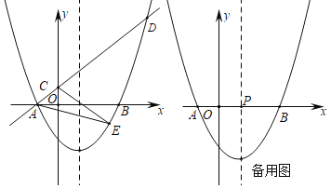
【题目】在平面直角坐标系中,将二次函数y=a![]() (a>0)的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧),OA=1,经过点A的一次函数
(a>0)的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧),OA=1,经过点A的一次函数![]() (
(![]() )的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E的坐标;
【答案】(1)![]() ,
,![]() ;(2)最大值是
;(2)最大值是![]() ,此时E点坐标为
,此时E点坐标为![]()
【解析】
(1)先写出平移后的抛物线解析式,经过点A(-1,0),可求得a的值,由△ABD的面积为5可求出点D的纵坐标,代入抛物线解析式求出横坐标,由A、D的坐标可求出一次函数解析式;
(2)作EM∥y轴交AD于M,如图,利用三角形面积公式,由![]() 构建二次函数,利用二次函数的性质即可解决问题;
构建二次函数,利用二次函数的性质即可解决问题;
(1)将二次函数![]() )的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
)的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为![]() ,
,
∵OA=1,
∴点A的坐标为(﹣1,0),代入抛物线的解析式得,![]() ,
,
∴![]() ,
,
∴抛物线的解析式为![]() ,即
,即![]() .
.
令y=0,解得![]() ,
,
∴点B的坐标为(3,0),
∴AB=OA+OB=4,
∵△ABD的面积为5,
∴![]() ,
,
∴![]() ,
,
代入抛物线解析式得,![]() ,
,
解得![]() ,
,
∴点D的坐标为(4,![]() ),
),
设直线AD的解析式为![]() ,
,
∴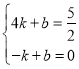 ,解得:
,解得:![]() ,
,
∴直线AD的解析式为![]() ;
;
(2)过点E作EM∥y轴交AD于M,交x轴于N,如图,
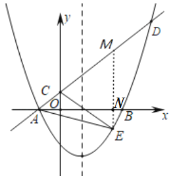
设点E的坐标为(![]() ,
,![]() ),则点M的坐标为(
),则点M的坐标为(![]() ,
,![]() )
)
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]() ,
,
∴当![]() 时,△ACE的面积有最大值,最大值是
时,△ACE的面积有最大值,最大值是![]() ,此时E点坐标为(
,此时E点坐标为( ![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
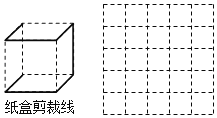
【题目】将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是 (填A或B).
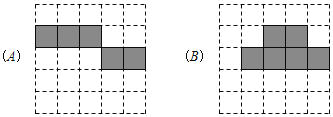
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)

(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满![]() 元,均可得到一次摸奖的机会.在一个纸盒里装有
元,均可得到一次摸奖的机会.在一个纸盒里装有![]() 个红球和
个红球和![]() 个白球(编号分别为红1、红
个白球(编号分别为红1、红![]() 、白1、白
、白1、白![]() ),除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如表)
),除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如表)
甲超市:
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
乙超市:
球 | 两红 | --红一白 | 两白 |
礼金券(元) |
|
|
|
(1)列举出一次摸奖时两球的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
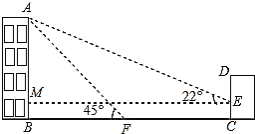
【题目】如图,某办公楼AB的右边有一建筑物CD,在建设物CD离地面2米高的点E处观测办公楼顶A点,测得的仰角![]() =
=![]() ,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角
,在离建设物CD 25米远的F点观测办公楼顶A点,测得的仰角![]() =
=![]() (B,F,C在一条直线上).
(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮晚上在广场散步,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
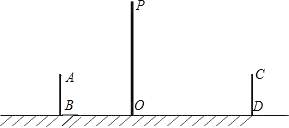
(1)请你在图中画出小亮站在AB处的影子BE;
(2)小亮的身高为1.6m,当小亮离开灯杆的距离OB为2.4m时,影长为1.2m,若小亮离开灯杆的距离OD=6m时,则小亮(CD)的影长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
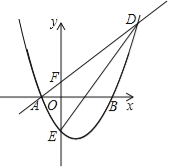
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
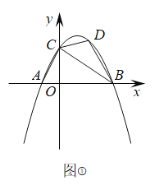

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com