
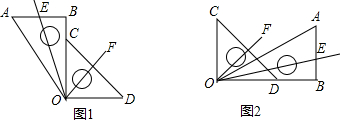
分析 (1)根据角平分线的定义和角的位置关系可以求得:∠AOE=∠EOB=$\frac{1}{2}$∠AOB,∠COF=∠FOD=$\frac{1}{2}$∠COD,再根据∠EOF=∠EOB+∠BOF可以求得∠EOF的度数;(2)根据角平分线的定义和角的位置关系可以求得:∠AOE=∠EOB=$\frac{1}{2}$∠AOB,∠COF=∠FOD=$\frac{1}{2}$∠COD,再根据∠EOF=∠BOF-∠BOE可以求得∠EOF的度数.
解答 解:(1)∵OE、OF平分∠AOB、∠COD,∠AOB=30°、∠COD=90°,
∴∠AOE=∠EOB=$\frac{1}{2}$∠AOB=15°,∠COF=∠FOD=$\frac{1}{2}$∠COD=45°,
∴∠EOF=∠EOB+∠BOF=15°+45°=60°;
(2)由(1)知∠EOF=∠BOF-∠BOE=45°-15°=30°;
归纳:若有公共定点的两个角∠α,∠β(∠α>∠β)有一条边重合,①当∠β的另一边在∠α外部时,两个角的平分线所夹的角的度数=$\frac{1}{2}(∠α+∠β)$;
②当∠β的另一边在∠α内部时,两个角的平分线所夹的角的度数=$\frac{1}{2}(∠α-∠β)$.
点评 此题主要考查了角的计算,关键是注意此题分两种情况.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:填空题
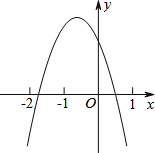 在平面直角坐标系中,如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标为x1、x2,其中-2<x1<-1,0<x2<1,则下列结论:
在平面直角坐标系中,如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标为x1、x2,其中-2<x1<-1,0<x2<1,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
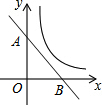 如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )
如图,直线y=k1x+b与坐标轴分别交于A(0,4),B(4,0)两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限,当这两个函数图象有公共点时,k2的最大整数值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{1}{2}$ | B. | x=$-\frac{1}{12}$ | C. | x=$\frac{1}{12}$ | D. | x=-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5ab-3ab=2 | B. | (1+$\sqrt{2}$)(1-$\sqrt{2}$)=1 | C. | -(-a)4÷a2=a2 | D. | (xy)-2=$\frac{1}{{x}^{2}{y}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
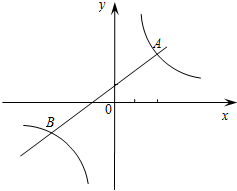 已知:如图,一次函数y=x+1与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象相交于点A(2,m)、B两点.
已知:如图,一次函数y=x+1与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象相交于点A(2,m)、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-3|=3 | B. | (-$\frac{1}{4}$)2=$\frac{1}{16}$ | C. | -$\frac{5}{3}+\frac{1}{3}=-\frac{4}{3}$ | D. | $\sqrt{{{({-2})}^2}}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
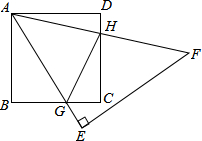 如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.
如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com