
【题目】如下图A1、A2、A3....在直线y=x上,点C1、C2、C3....在直线y=2x上,以它们为顶点依次构造第一个正方形A1C1A2B1,第二个正方形A2C2A3B2...,若A1的横坐标是1,则B3的坐标是__________,第n个正方形的面积是__________.

【答案】(8,4). 22n-2
【解析】
由A1的横坐标是1,可得A1(1,1),利用函数解析式求出点C1的坐标,得出A1C1的长度以及第1个正方形的面积,求出B1的坐标;然后再求出C2的坐标,得出第2个正方形的面积,求出B2的坐标;再求出B3、C3的坐标,得出第3个正方形的面积;从而得出规律即可得到第n个正方形的面积.
解:∵点A1、A2、A3…在直线y=x上,A1的横坐标是1,
∴A1(1,1),
∵点C1,C2,C3…在直线y=2x上,
∴C1(1,2),A1(1,1),
∴A1C1=2-1=1,B1(2,1),
∴第1个正方形的面积为:12;
∵C2(2,4),
∴A2C2=4-2=2,B2(4,2),A3(4,4),
∴第2个正方形的面积为:22;
∵C3(4,8),
∴A3C3=8-4=4,B3(8,4),
∴第3个正方形的面积为:24;
…,
∴第n个正方形的面积为:(2n-1)2=22n-2.
故答案为(8,4),22n-2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
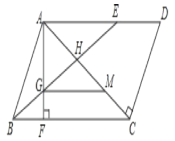
(1)若∠D=50°,求∠EBC的度数;
(2)若AC⊥CD,过点G作GM∥BC交AC于点M,求证:AH=MC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在校园文化艺术节期间,举办了歌咏、小品、书法、绘画共四个项目的比赛,要求每名学生必须参加且仅参加一项.小明随机调查了部分学生的报名情况,根据调查结果绘制出了如下不完整的“各项目参赛人数及比例”统计表,请根据图表中提供的信息,解答下列的问题:
(1)本次调查中共抽取了___________名学生;
(2)表中的![]() _________,
_________,![]() __________;
__________;
(3)根据统计表中的数据和所学统计图的知识,任选绘制一幅统计图,能直观反映各项目的参加人数或参赛人数的比例.
各项目参赛人数及比例统计表
项目 | 人数 | 百分比 |
歌咏 | 20 |
|
小品 | 60 |
|
书法 |
|
|
绘画 | 40 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
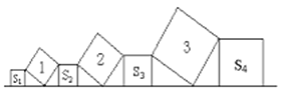
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
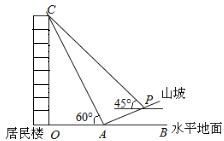
【题目】如图 ,一幢居民楼OC临近山坡AP,山坡AP的坡度为i=1:![]() ,小亮在距山坡坡脚A处测得楼顶C 的仰角为60°,当从A 处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为 45°,点 O,A,B 在同一直线上,求该居民楼的高度.(结果保留整数,
,小亮在距山坡坡脚A处测得楼顶C 的仰角为60°,当从A 处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为 45°,点 O,A,B 在同一直线上,求该居民楼的高度.(结果保留整数,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有着丰富的土地资源,适宜种植玉米,某企业已收购玉米52.5吨,根据市场信息,将玉米直接销售,每吨可获利100元;如果对玉米进行粗加工,每天可加工8吨,每吨可获利1000元;如果对玉米进行精加工,每天可加工0.5吨,每吨可获利5000元.由于受条件限制,在同一天中只能采取一种加工方式,并且必须在30天内将这批玉米全部销售,为此,研究了两种方案.
(1)方案一:将玉米全部粗加工后销售,则可获利 元;
(2)方案二:30天时间都进行精加工,未来得及加工的玉米,在市场上直接销售,则可获利 元;
(3)问是否存在第三种方案,将部分玉米精加工,其余玉米粗加工,并恰好在30天内完成?若存在,请求销售后所获利润:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
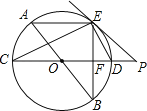
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com