
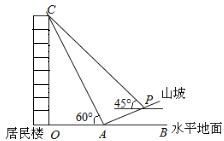
【题目】如图 ,一幢居民楼OC临近山坡AP,山坡AP的坡度为i=1:![]() ,小亮在距山坡坡脚A处测得楼顶C 的仰角为60°,当从A 处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为 45°,点 O,A,B 在同一直线上,求该居民楼的高度.(结果保留整数,
,小亮在距山坡坡脚A处测得楼顶C 的仰角为60°,当从A 处沿坡面行走10米到达P处时,测得楼顶C的仰角刚好为 45°,点 O,A,B 在同一直线上,求该居民楼的高度.(结果保留整数,![]() ≈1.73)
≈1.73)
【答案】32
【解析】分析:作PE⊥OB于点E,PF⊥CO于点F,如图,设PE=x,则AE=![]() x,在Rt△AEP中根据勾股定理可得PE=5,则AE=
x,在Rt△AEP中根据勾股定理可得PE=5,则AE=![]() ;设CF=PF=m米,则OC=(m+5)米、OA=(m- -
;设CF=PF=m米,则OC=(m+5)米、OA=(m- -![]() )米,在Rt△AOC中,由tan60°=
)米,在Rt△AOC中,由tan60°=![]() 求得m的值,继而可得答案.
求得m的值,继而可得答案.
详解:过点P作PE⊥OB交OB于点E,PF⊥OC交OC于点F,
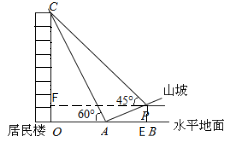
∵i=1:![]() , AP=10
, AP=10
设PE=x,则AE=![]() x,
x,
在Rt△AEP中,x2+(![]() x)2=102,
x)2=102,
解得:x=5或x=-5(舍),
∴PE=5,则AE=![]() ,
,
∵∠CPF=∠PCF=45°,
∴CF=PF,
设CF=PF=m米,则OC=(m+5)米,OA=(m-![]() )米,
)米,
在Rt△AOC中,![]() ,即
,即![]() ,
,
解得:m=10(![]() +1),
+1),
∴OC=10(![]() +1)+5≈32米,
+1)+5≈32米,
答:塑像的高度约为32米.


科目:初中数学 来源: 题型:
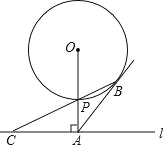
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:反比例函数y=![]() 的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.
的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.
(1)求k,b的值;
(2)若一次函数y=ax+1的图象经过点A,且与x轴交于M,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,CD是中线,
,CD是中线,![]() ,一个以点D为顶点的
,一个以点D为顶点的![]() 角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.

![]() 如图1,若
如图1,若![]() ,求证:
,求证:![]() ;
;
![]() 如图2,在
如图2,在![]() 绕点D旋转的过程中:
绕点D旋转的过程中:
![]() 探究三条线段AB,CE,CF之间的数量关系,并说明理由;
探究三条线段AB,CE,CF之间的数量关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求DN的长.
,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图A1、A2、A3....在直线y=x上,点C1、C2、C3....在直线y=2x上,以它们为顶点依次构造第一个正方形A1C1A2B1,第二个正方形A2C2A3B2...,若A1的横坐标是1,则B3的坐标是__________,第n个正方形的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个) 的变化如下表:同时,销售过程中的其他开支(不含进价)总计40万元.
销售价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)观察并分析表中的数据,用所学过的函数知识,直接写出y与 x的函数解析式;
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格 x(元/个) 的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请你结合函数图象求出销售价格 x(元/个) 的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1)l1和l2哪一条是描述小凡的运动过程,说说你的理由;
(2)小凡和小光谁先出发,先出发了多少分钟?
(3)小凡与小光谁先到达图书馆,先到了多少分钟?
(4)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间) 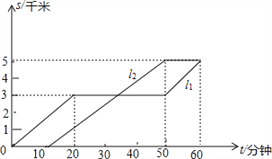
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(观察发现):(1)如图1,四边形ABCD和四边形AEFG都是正方形,且点E在边AB上,连接DE和BG,猜想线段DE与BG的数量关系和位置关系.(只要求写出结论,不必说出理由)
(深入探究):(2)如图2,将图1中正方形AEFG绕点A逆时针旋转一定的角度,其他条件与观察发现中的条件相同,观察发现中的结论是否还成立?请根据图2加以说明.
(拓展应用):(3)如图3,直线l上有两个动点A、B,直线l外有一点动点Q,连接QA,QB,以线段AB为边在l的另一侧作正方形ABCD,连接QD.随着动点A、B的移动,线段QD的长也会发生变化,若QA,QB长分别为3![]() ,6保持不变,在变化过程中,线段QD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
,6保持不变,在变化过程中,线段QD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:形如![]() 为常数,
为常数,![]() 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当![]() 时,“奇特函数”
时,“奇特函数”![]() 就是反比例函数
就是反比例函数![]() .
.
(1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”;
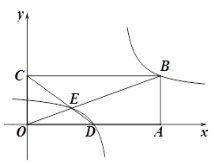
(2) 如图,点O为坐标原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3).点D是OA的中点,连结OB,CD交于点E,“奇特函数”![]() 的图象经过B,E两点.
的图象经过B,E两点.
① 求这个“奇特函数”的解析式;
② 把反比例函数![]() 的图象向右平移6个单位,再向上平移 个单位可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点(P在Q的右侧),若以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标.
的图象向右平移6个单位,再向上平移 个单位可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点(P在Q的右侧),若以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com