
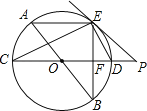
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)如图,连接OE,证明OE⊥PE即可得出PE是⊙O的切线;
(2)由圆周角定理得到∠AEB=∠CED=90°,进而得到∠3=∠4,结合已知条件证得结论;
(3)设EF=x,则CF=2x,在RT△OEF中,根据勾股定理求出EF的长,进而求得BE,CF的长,在RT△AEB中,根据勾股定理求出AE的长,然后根据△AEB∽△EFP,求出PF的长,即可求得PD的长.
试题解析:(1)如图,连接OE.∵CD是圆O的直径,∴∠CED=90°,∵OC=OE,∴∠1=∠2,又∵∠PED=∠C,即∠PED=∠1,∴∠PED=∠2,∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,∴OE⊥EP,又∵点E在圆上,∴PE是⊙O的切线;
(2)∵AB、CD为⊙O的直径,∴∠AEB=∠CED=90°,∴∠3=∠4(同角的余角相等),又∵∠PED=∠1,∴∠PED=∠4,即ED平分∠BEP;
(3)设EF=x,则CF=2x,∵⊙O的半径为5,∴OF=2x﹣5,在RT△OEF中,![]() ,即
,即![]() ,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴
,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴![]() ,即
,即![]() ,∴PF=
,∴PF=![]() ,∴PD=PF﹣DF=
,∴PD=PF﹣DF=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如下图A1、A2、A3....在直线y=x上,点C1、C2、C3....在直线y=2x上,以它们为顶点依次构造第一个正方形A1C1A2B1,第二个正方形A2C2A3B2...,若A1的横坐标是1,则B3的坐标是__________,第n个正方形的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
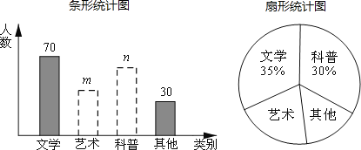
【题目】在“书香包河”读书活动中,学校准备购买一批课外读物,为使课外读物满足学生们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了______________名同学;
(2)条形统计图中,m=_________,n=__________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过某矩形的两个相对的顶点作平行线,再沿着平行线剪下两个直角三角形,剩余的图形为如图所示的ABCD,AB=4,BC=6,∠ABC=60°,则原来矩形的面积是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:形如![]() 为常数,
为常数,![]() 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当![]() 时,“奇特函数”
时,“奇特函数”![]() 就是反比例函数
就是反比例函数![]() .
.
(1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”;
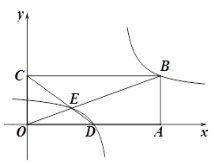
(2) 如图,点O为坐标原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3).点D是OA的中点,连结OB,CD交于点E,“奇特函数”![]() 的图象经过B,E两点.
的图象经过B,E两点.
① 求这个“奇特函数”的解析式;
② 把反比例函数![]() 的图象向右平移6个单位,再向上平移 个单位可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点(P在Q的右侧),若以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标.
的图象向右平移6个单位,再向上平移 个单位可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点(P在Q的右侧),若以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
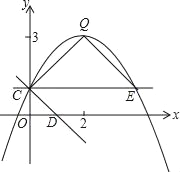
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
快放寒假了,小宇来到书店准备购买一些课外读物在假期里阅读.在选完书结账时,收银员告诉小宇,如果花20元办理一张会员卡,用会员卡结账买书,可以享受8折优惠.小宇心算了一下,觉得这样可以节省13元,很合算,于是采纳了收银员的意见.请根据以上信息解答下列问题:
(1)你认为小宇购买 元以上的书,办卡就合算了;
(2)小宇购买这些书的原价是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABE和等腰三角形ADF.
(1)当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABE和等腰直角△ADF,连接BF、ED,线段BF和ED的数量关系是_____________;
(2)当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABE和等腰直角△ADF,连接EF、BD,线段EF和BD具有怎样的数量关系?请说明理由;
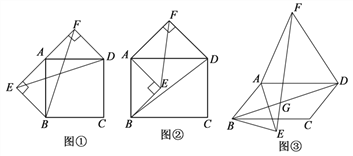
(3)当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABE和等腰△ADF,且△ABE和△ADF的顶角均为![]() ,连接EF、BD,交点为G.请用
,连接EF、BD,交点为G.请用![]() 表示出∠FGD,并说明理由.
表示出∠FGD,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com