Question

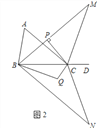
【题目】如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE、BD．

（1）猜想PM与PN的数量关系及位置关系，请直接写出结论；
（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP、BD分别交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；

（3）若图②中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图③，写出PM与PN的数量关系，并加以证明．

Answer 1

【答案】
（1）

解：PM=PN，PM⊥PN，理由如下：

∵△ACB和△ECD是等腰直角三角形，

∴AC=BC，EC=CD，∠ACB=∠ECD=90°．

在△ACE和△BCD中

，

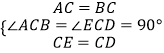∴△ACE≌△BCD（SAS），

∴AE=BD，∠EAC=∠CBD，

∵点M、N分别是斜边AB、DE的中点，点P为AD的中点，

∴PM= BD，PN= AE，

∴PM=PM，

∵PM∥BD，PN∥AE，AE⊥BD，

∴∠NPD=∠EAC，∠MPA=∠BDC，∠EAC+∠BDC=90°，

∴∠MPA+∠NPC=90°，

∴∠MPN=90°，

即PM⊥PN；

（2）

解：∵△ACB和△ECD是等腰直角三角形，

∴AC=BC，EC=CD，

∠ACB=∠ECD=90°．

∴∠ACB+∠BCE=∠ECD+∠BCE．

∴∠ACE=∠BCD．

∴△ACE≌△BCD．

∴AE=BD，∠CAE=∠CBD．

又∵∠AOC=∠BOE，

∠CAE=∠CBD，

∴∠BHO=∠ACO=90°．

∵点P、M、N分别为AD、AB、DE的中点，

∴PM= BD，PM∥BD；

PN= AE，PN∥AE．

∴PM=PN．

∴∠MGE+∠BHA=180°．

∴∠MGE=90°．

∴∠MPN=90°．

∴PM⊥PN．

（3）

解：PM=kPN

∵△ACB和△ECD是直角三角形，

∴∠ACB=∠ECD=90°．

∴∠ACB+∠BCE=∠ECD+∠BCE．

∴∠ACE=∠BCD．

∵BC=kAC，CD=kCE，

∴ =k．

∴△BCD∽△ACE．

∴BD=kAE．

∵点P、M、N分别为AD、AB、DE的中点，

∴PM= BD，PN= AE．

∴PM=kPN．

【解析】（1）由等腰直角三角形的性质易证△ACE≌△BCD，由此可得AE=BD，再根据三角形中位线定理即可得到PM=PN，由平行线的性质可得PM⊥PN；（2）（1）中的结论仍旧成立，由（1）中的证明思路即可证明；（3）PM=kPN，由已知条件可证明△BCD∽△ACE，所以可得BD=kAE，因为点P、M、N分别为AD、AB、DE的中点，所以PM= BD，PN= AE，进而可证明PM=kPN．