
【题目】探究函数y=x+ ![]() 的图象与性质
的图象与性质
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中,函数y=x+ ![]() 的图象大致是
的图象大致是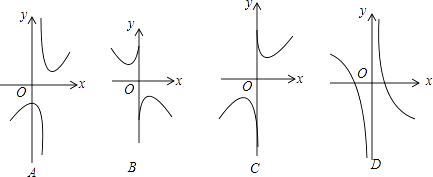
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下面求解此问题的过程补充完整:
解:∵x>0
∴y=x+ ![]()
=( ![]() )2+(
)2+( ![]() )2
)2
=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0,
)2≥0,
∴y .
(4)若函数y= ![]() ,则y的取值范围是
,则y的取值范围是
【答案】
(1)x≠0
(2)C
(3)6;≥6
【拓展运用】
(4)y≤﹣11或y≥1
【解析】解:(1)∵在y=x+ ![]() 中,x≠0,
中,x≠0,
∴x的取值范围是x≠0.
所以答案是:x≠0.(2)∵x≠0,
∴A中图象不符合题意;
∵当x>0时,x+ ![]() >0,
>0,
当x<0时,x+ ![]() <0,
<0,
∴函数y=x+ ![]() 的图象在第一、三象限,
的图象在第一、三象限,
∴B、D中图象不符合题意,
故选C.(3)解:∵x>0,
∴y=x+ ![]() ,
,
=( ![]() )2+(
)2+( ![]() )2 ,
)2 ,
=( ![]() ﹣
﹣ ![]() )2+6,
)2+6,
∵( ![]() ﹣
﹣ ![]() )2≥0,
)2≥0,
∴y≥6.
所以答案是:6;≥6.(4)y= ![]() =x+
=x+ ![]() ﹣5.
﹣5.
由(3)可知:当x>0时,x+ ![]() ≥6;
≥6;
当x<0时,x+ ![]() ≤﹣6.
≤﹣6.
∴y=x+ ![]() ﹣5≥6﹣5=1,y=x+
﹣5≥6﹣5=1,y=x+ ![]() ﹣5≤﹣6﹣5=﹣11.
﹣5≤﹣6﹣5=﹣11.
y的取值范围是y≤﹣11或y≥1.
所以答案是:y≤﹣11或y≥1.
【考点精析】根据题目的已知条件,利用反比例函数的性质的相关知识可以得到问题的答案,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为CD上一点,连接AE、BD , 且AE、BD交于点F , DE:EC=2:3,则S△DEF:S△ABF=( ) 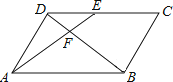
A.2:3
B.4:9
C.2:5
D.4:25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°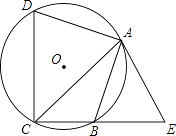
(1)求证:AE是⊙O的切线;
(2)若 AB=AD,AC=2 ![]() ,tan∠ADC=3,求CD的长.
,tan∠ADC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8. 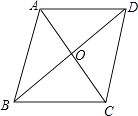
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.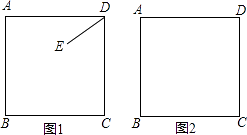
(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG= ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2). 
(1)求这两个函数的表达式;
(2)观察图象,直接写出y1>y2时自变量x的取值范围.
(3)连接OA、OB,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com