
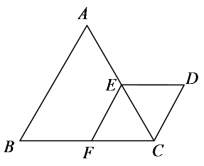
【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB.
(1)求证:四边形EFCD是菱形;
(2)设CD=2,求D、F两点间的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)由等边三角形的性质得出ED=CD=CE,证出△CEF是等边三角形,得出EF=CF=CE,得出ED=CD=EF=CF,即可得出结论;
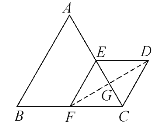
(2)连接DF,与CE相交于点G,根据菱形的性质求出DG,即可得出结果.
(1)证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD=CE,∠A=∠B=∠BCA=60°.
∴EF∥AB.
∴∠CEF=∠A=60°,∠CFE=∠B=60°,
∴∠CEF=∠CFE=∠ACB,
∴△CEF是等边三角形,
∴EF=CF=CE,
∴ED=CD=EF=CF,
∴四边形EFCD是菱形.
(2)连接DF与CE交于点G
∵四边形EFCD是菱形
∴DF⊥CE, DF=2DG
∵CD=2,△EDC是等边三边形
∴CG=1,DG=![]()
∴DF=2DG=![]() ,即D、F两点间的距离为
,即D、F两点间的距离为![]()


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
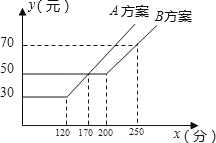
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
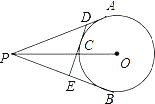
【题目】如图,PA、PB切⊙O于A.B,点C在AB上,DE切⊙O于C,交PA、PB于D.E,已知PO=5cm,⊙O的半径为3cm,则△PDE的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,
,![]() 的面积为48.
的面积为48.
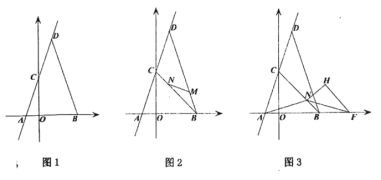
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,连接
上,连接![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,如图3,连接![]() ,点
,点![]() 为
为![]() 轴正半轴上点
轴正半轴上点![]() 右侧一点,点
右侧一点,点![]() 为第一象限内一点,
为第一象限内一点,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,直线
上一点,直线![]() 经过点
经过点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,请你判断四边形
,请你判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
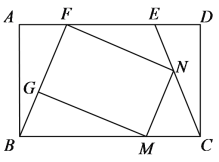
【题目】如图,在矩形ABCD中,点E、F在边AD上,AF=DE,连接BF、CE.
(1)求证:∠CBF=∠BCE;
(2)若点G、M、N在线段BF、BC、CE上,且 FG=MN=CN.求证:MG=NF;
(3)在(2)的条件下,当∠MNC=2∠BMG时,四边形FGMN是什么图形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋中有3张形状大小完全相同的卡片,编号为1、2、3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率;
(3)任选一个符合(2)题条件的方程,设此方程的两根为x1、x2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是直角梯形,AB=18cm,CD=15cm,AD=6cm,点P从B点开始,沿BA边向点A以1cm/s的速度移动,点Q从D点开始,沿DC边向点C以2cm/s的速度移动,如果P、Q分别从B、D同时出发,P、Q有一点到达终点时运动停止,设移动时间为t.
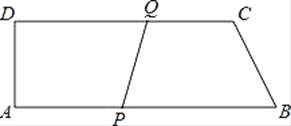
(1)t为何值时四边形PQCB是平行四边形?
(2)t为何值时四边形PQCB是矩形?
(3)t为何值时四边形PQCB是等腰梯形?
查看答案和解析>>
科目:初中数学 来源: 题型:
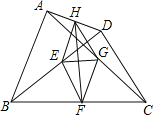
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com