
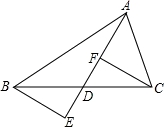
如图,已知:AD是BC上的中线,且DF=DE.求证:BE∥CF.
【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】欲证BE∥CF,需先证得∠EBC=∠FCD或∠E=∠CFD,那么关键是证△BED≌△CFD;这两个三角形中,已知的条件有:BD=DC,DE=DF,而对顶角∠BDE=∠CDF,根据SAS即可证得这两个三角形全等,由此可得出所证的结论.
【解答】证明:∵AD是BC上的中线,
∴BD=DC.
又∵DF=DE(已知),
∠BDE=∠CDF(对顶角相等),
∴△BED≌△CFD(SAS).
∴∠E=∠CFD(全等三角形的对应角相等).
∴CF∥BE(内错角相等 ,两直线平行).
,两直线平行).
【点评】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.


科目:初中数学 来源: 题型:
请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )
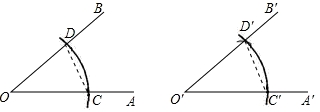
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图:某地有两所大学和两条相交叉的公路(点M,N表示大学,AO,BO表示公路).现计划修建一座仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案(要求保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
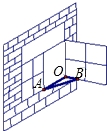
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com