Question

【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为： ．
②BC，CD，CF之间的数量关系为：；（将结论直接写在横线上）

（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

（3）拓展延伸
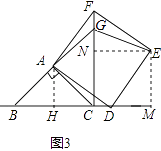
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2 ，CD= BC，请求出GE的长．

Answer 1

【答案】
（1）垂直；BC=CD+CF
（2）

解：CF⊥BC成立；BC=CD+CF不成立，CD=CF+BC．

∵正方形ADEF中，AD=AF，

∵∠BAC=∠DAF=90°，

∴∠BAD=∠CAF，

在△DAB与△FAC中， ，

∴△DAB≌△FAC，

∴∠ABD=∠ACF，

∵∠BAC=90°，AB=AC，

∴∠ACB=∠ABC=45°．

∴∠ABD=180°﹣45°=135°，

∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°，

∴CF⊥BC．

∵CD=DB+BC，DB=CF，

∴CD=CF+BC．

（3）

解：过A作AH⊥BC于H，过E作EM⊥BD于M，EN⊥CF于N，

∵∠BAC=90°，AB=AC，

∴BC= AB=4，AH= BC=2，

∴CD= BC=1，CH= BC=2，

∴DH=3，

由（2）证得BC⊥CF，CF=BD=5，

∵四边形ADEF是正方形，

∴AD=DE，∠ADE=90°，

∵BC⊥CF，EM⊥BD，EN⊥CF，

∴四边形CMEN是矩形，

∴NE=CM，EM=CN，

∵∠AHD=∠ADE=∠EMD=90°，

∴∠ADH+∠EDM=∠EDM+∠DEM=90°，

∴∠ADH=∠DEM，

在△ADH与△DEM中， ，

∴△ADH≌△DEM，

∴EM=DH=3，DM=AH=2，

∴CN=EM=3，EN=CM=3，

∵∠ABC=45°，

∴∠BGC=45°，

∴△BCG是等腰直角三角形，

∴CG=BC=4，

∴GN=1，

∴EG= = ．

【解析】解：（1）①正方形ADEF中，AD=AF，
∵∠BAC=∠DAF=90°，
∴∠BAD=∠CAF，
在△DAB与△FAC中， ，
∴△DAB≌△FAC，
∴∠B=∠ACF，
∴∠ACB+∠ACF=90°，即BC⊥CF；
故答案为：垂直；②△DAB≌△FAC，
∴CF=BD，
∵BC=BD+CD，
∴BC=CF+CD；
故答案为：BC=CF+CD；
（1）①根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB≌△FAC，根据全等三角形的性质即可得到结论；②由正方形ADEF的性质可推出△DAB≌△FAC，根据全等三角形的性质得到CF=BD，∠ACF=∠ABD，根据余角的性质即可得到结论；（2）根据正方形的性质得到∠BAC=∠DAF=90°，推出△DAB≌△FAC，根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论．（3）根据等腰直角三角形的性质得到BC= AB=4，AH= BC=2，求得DH=3，根据正方形的性质得到AD=DE，∠ADE=90°，根据矩形的性质得到NE=CM，EM=CN，由角的性质得到∠ADH=∠DEM，根据全等三角形的性质得到EM=DH=3，DM=AH=2，等量代换得到CN=EM=3，EN=CM=3，根据等腰直角三角形的性质得到CG=BC=4，根据勾股定理即可得到结论．