
【题目】如图,在△ABC中,∠BAC=90°,∠ACB=30°,BC=8,以BC为边,在△ABC外作等边△BCD,点E为BC中点,连接AE并延长交CD于点F.
(1)求证:四边形ABDF是平行四边形;
(2)如图2,将图1中的ABCD折叠,使点D和点A重合,折痕为GH,求CG的长.
【答案】
(1)
证明:∵∠BAC=90°,点E为BC中点,
∴AE= ![]() BC=BE,
BC=BE,
∵∠ACB=30°,
∴∠ABC=60°,
∴△ABE是等边三角形,
∴∠AEB=60°,
∵△BCD是等边三角形,
∴∠DBC=∠BCD=60°,
∴∠ACD=∠ACB+∠BCD=30°+60°=90°,
∵∠DBC=∠AEB=60°,∠BAC=∠ACD=90°,
∴AB∥CD,BD∥AF,
∴四边形ABDF是平行四边形
(2)
解:∵∠BAC=90°,∠ACB=30°,BC=8,
∴AB=4,AC= ![]() =
= ![]() =4
=4 ![]() ,
,
∵△BCD是等边三角形,
∴CD=BC=8,
设CG=x,则DG=8﹣x,
在Rt△ACG中,AG2=AC2+CG2,
即:(8﹣x)2=x2+(4 ![]() )2,
)2,
解得:x=1,
∴CG=1
【解析】(1)先证明△ABE是等边三角形,得出∠AEB=60°,由△BCD是等边三角形,得出∠DBC=∠BCD=60°,∠ACD=90°,证得AB∥CD,BD∥AF,即可得出结论;(2)求出AB=4,AC=4 ![]() ,设CG=x,则DG=8﹣x,在Rt△ACG中,AG2=AC2+CG2 , 代入解方程即可得出结果.
,设CG=x,则DG=8﹣x,在Rt△ACG中,AG2=AC2+CG2 , 代入解方程即可得出结果.
【考点精析】通过灵活运用等边三角形的性质和直角三角形斜边上的中线,掌握等边三角形的三个角都相等并且每个角都是60°;直角三角形斜边上的中线等于斜边的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2. 
(1)若DG=6,求AE的长;
(2)若DG=2,求证:四边形EFGH是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.

(1)求证:△BEC∽△ABF;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用三角板工具画角很方便,但是只能画出一些特殊的角,下列角度不能用一副三角板(不再用其他工具)画出的是( )
A. 15°B. 20°C. 75°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个完全相同的标有数字1、2、3、4的小球. 小明从布袋里随机取出一个小球,记下数字为x,小红从布袋里剩下的小球中随机取出一个,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形的上底长是![]() 厘米,下底长是
厘米,下底长是![]() 厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
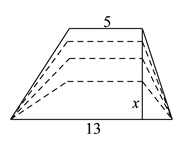
(![]() )在这个变化过程中,自变量是__________,因变量是__________.
)在这个变化过程中,自变量是__________,因变量是__________.
(![]() )梯形的面积
)梯形的面积![]() 与高
与高![]() (厘米)之间的关系式为__________.
(厘米)之间的关系式为__________.
(![]() )当梯形的高由
)当梯形的高由![]() 厘米变化到
厘米变化到![]() 厘米时,梯形的面积由__________
厘米时,梯形的面积由__________![]() 变化到__________
变化到__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长方形的长是![]() ,宽是,周长是
,宽是,周长是![]() ,面积是
,面积是![]() .
.
(1)写出![]() 随
随![]() 变化而变化的关系式;
变化而变化的关系式;
(2)写出![]() 随
随![]() 变化而变化的关系式;
变化而变化的关系式;
(3)当![]() 时,
时, ![]() 等于多少?
等于多少? ![]() 等于多少?
等于多少?
(4)当![]() 增加
增加![]() 时,
时, ![]() 增加多少?
增加多少? ![]() 增加多少?
增加多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O 
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com