
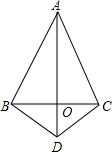
 如图,在△ABC中,AB=AC,点O是BC的中点,连接AO,在AO的延长线上取一点D,连接BD,CD
如图,在△ABC中,AB=AC,点O是BC的中点,连接AO,在AO的延长线上取一点D,连接BD,CD分析 (1)利用全等三角形的判定方法结合SAS得出即可;
(2)利用菱形的判定方法对角线互相垂直且平分的四边形是菱形得出即可.
解答 (1)证明:∵AB=AC,点O是BC的中点,
∴∠BAO=∠CAO,
在△ABD和△ACD中
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(SAS);
(2)解:当AO=$\frac{1}{2}$AD时,四边形ABDC是菱形.
理由:∵AO=$\frac{1}{2}$AD,∴AO=DO,
又∵BO=CO,AO⊥BC,
∴四边形ABDC是菱形.
点评 此题主要考查了菱形的判定以及全等三角形的判定与性质,熟练应用全等三角形的判定方法是解题关键.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:选择题
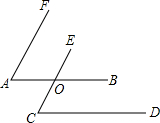 如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )
如图,∠FAB与∠ECD都是锐角,其中AB∥CD,AF∥CE,射线AB与CE相交于点O,若∠FAB=60°,则∠ECD的度数是( )| A. | 30° | B. | 60° | C. | 80° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)(b-a) | B. | (-1-a)(a+1) | C. | (-m+n)(-m-n) | D. | (ax+b)(n-bx) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,结合图象解答下列问题:
快、慢两车分别从相距480km的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留了1小时,然后继续以原速驶向甲地,到达甲地后即停止行驶;快车到达乙地后,立即按原路原速返回甲地(调头时间忽略不计).如图是快、慢两车距乙地路程y(km)与所用时间x(h)之间的函数图象,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
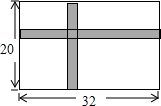 校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2,小道的宽应是2米.
校生物小组有一块长32m,宽20m的矩形实验田,为了管理方便,准备沿平行于两边的方向纵、横个开辟一条等宽的小道,要使种植面积为540m2,小道的宽应是2米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com