
 如图,直线l1,l2分别与另两条直线相交,已知∠1=∠2,求证:∠3+∠4=180°.
如图,直线l1,l2分别与另两条直线相交,已知∠1=∠2,求证:∠3+∠4=180°. 科目:初中数学 来源: 题型:解答题
 如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD的高度为多少?(保留根号)
如图所示,河对岸有水塔CD.今在A处测得塔顶C的仰角为30°,前进20米到达B处,又测得C的仰角为45°,则塔高CD的高度为多少?(保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
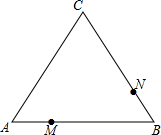 如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.
如图,在△ABC中,AB=30cm,BC=35cm,∠B=60°,有一动点M自A向B以1cm/s的速度运动,动点N自B向C以2cm/s的速度运动,若M,N同时分别从A,B出发.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AD、AE分别是BC边上的中线和高,点F是AB中点,作FH⊥BC于点H,FH与AD的延长线交于点G.若AC=$\sqrt{34}$,tan∠ABC=$\frac{4}{5}$,DE=FH,则HG=$\sqrt{2}$.
如图,△ABC中,AD、AE分别是BC边上的中线和高,点F是AB中点,作FH⊥BC于点H,FH与AD的延长线交于点G.若AC=$\sqrt{34}$,tan∠ABC=$\frac{4}{5}$,DE=FH,则HG=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | BC=CH |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com