练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图所示，河对岸有水塔CD．今在A处测得塔顶C的仰角为30°，前进20米到达B处，又测得C的仰角为45°，则塔高CD的高度为多少？（保留根号）

    分析 设CD=x米，根据等腰直角三角形的性质求出BD，根据正切的概念求出AD，结合图形列出方程，解方程即可．

    解答 解：设CD=x米，
    在Rt△CBD中，∠CBD=45°，
    ∴BD=CD=x．
    在Rt△ACD中，∠CAD=30°，
    ∴AD=$\sqrt{3}$x．
    ∵AB=20，
    ∴AD=x+20．
    ∴x+20=$\sqrt{3}$x，
    解得，x=10（$\sqrt{3}$+1），
    答：塔高CD的高度为10（$\sqrt{3}$+1）米．

    点评 本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．关于二次函数y=-2x2+3，下列说法中正确的是（　　）
    A．它的开口方向是向上B．当x＜-1时，y随x的增大而增大
    C．它的顶点坐标是（-2，3）D．它的对称轴是x=-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图：列车6258次从福利屯到佳木斯途经笔架山、丰乐镇、太平镇、四马架四个停靠车站，两站之间的距离各不相同，则福利屯至佳木斯和沿途车站售票员应共准备单程15种火车票（假设没有异地售票）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．用度分秒表示：112.17°=112°10′12″．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．当x=1时，代数式mx3+nx+1的值为2009，当x=-1时，mx3+nx+1的值为（　　）
    A．-2008B．-2007C．-2009D．2007

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．在下列数：-1.414，-$\sqrt{2}$，$\frac{22}{7}$，111000中，是无理数的是（　　）
    A．-1.414B．-$\sqrt{2}$C．$\frac{22}{7}$D．111000

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．计算（-2）×3的结果是（　　）
    A．-5B．-6C．1D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

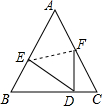    16．如图所示，△ABC是等边三角形，点D为AB上一点，现将△ABC沿EF折叠，使得顶点A与D点重合，且FD⊥BC，则$\frac{AE}{AF}$的值等于（　　）
    A．$\frac{4}{3}$B．$\frac{{2\sqrt{3}}}{3}$C．$\frac{{\sqrt{2}+1}}{3}$D．$\frac{{\sqrt{3}+1}}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，直线l1，l2分别与另两条直线相交，已知∠1=∠2，求证：∠3+∠4=180°．

    查看答案和解析>>

    同步练习册答案