
ЁОЬтФПЁПЙлВьгыЫМПМЃКдФЖСЯТСаВФСЯЃЌВЂНтОіКѓУцЕФЮЪЬт
дкШёНЧЁїABCжаЃЌЁЯAЁЂЁЯBЁЂЁЯCЕФЖдБпЗжБ№ЪЧaЁЂbЁЂcЃЌЙ§AзїADЁЭBCгкDЃЈШчЭМ(1)ЃЉЃЌдђsinB=![]() ЃЌsinC=
ЃЌsinC=![]() ЃЌМДADЃНcsinBЃЌADЃНbsinCЃЌгкЪЧcsinBЃНbsinCЃЌМД
ЃЌМДADЃНcsinBЃЌADЃНbsinCЃЌгкЪЧcsinBЃНbsinCЃЌМД![]() ЃЌЭЌРэгаЃК
ЃЌЭЌРэгаЃК![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЎ
ЃЎ
МДЃКдквЛИіШ§НЧаЮжаЃЌИїБпКЭЫќЫљЖдНЧЕФе§ЯвЕФБШЯрЕШдкШёНЧШ§НЧаЮжаЃЌШєвбжЊШ§ИідЊЫиЃЈжСЩйгавЛЬѕБпЃЉЃЌдЫгУЩЯЪіНсТлКЭгаЙиЖЈРэОЭПЩвдЧѓГіЦфгрШ§ИіЮДжЊдЊЫиЃЎ
ИљОнЩЯЪіВФСЯЃЌЭъГЩЯТСаИїЬтЃЎ

(1)ШчЭМ(2)ЃЌЁїABCжаЃЌЁЯBЃН45ЁуЃЌЁЯCЃН75ЁуЃЌBCЃН60ЃЌдђЁЯAЃНЁЁ ЁЁЃЛACЃНЁЁ ЁЁЃЛ
(2)здДгШЅФъШеБОеўИЎзджїздЕМЁАЕігуЕКЙњгаЛЏЁБФжОчвдРДЃЌЮвЙњеўИЎСщЛюгІЖдЃЌЯжШчНёвбЖдЕігуЕКжДааГЃЬЌЛЏбВТпЃЎФГДЮбВТпжаЃЌШчЭМЃЈ3ЃЉЃЌЮвгцеў204ДЌдкCДІВтЕУAдкЮвгцеўДЌЕФББЦЋЮї30ЁуЕФЗНЯђЩЯЃЌЫцКѓвд40КЃРя/ЪБЕФЫйЖШАДББЦЋЖЋ30ЁуЕФЗНЯђКНааЃЌАыаЁЪБКѓЕНДяBДІЃЌДЫЪБгжВтЕУЕігуЕКAдкЕФББЦЋЮї75ЁуЕФЗНЯђЩЯЃЌЧѓДЫЪБгцеў204ДЌОрЕігуЕКAЕФОрРыABЃЎЃЈНсЙћОЋШЗЕН0.01ЃЌ![]() Ёж2.449ЃЉ
Ёж2.449ЃЉ
ЁОД№АИЁПЃЈ1ЃЉ60ЃЌ20![]() ЃЛЃЈ2ЃЉгцеўДЌОрКЃЕКAЕФОрРыABдМЮЊ24.49КЃРяЃЎ
ЃЛЃЈ2ЃЉгцеўДЌОрКЃЕКAЕФОрРыABдМЮЊ24.49КЃРяЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЬтФПзмНсЕФе§ЯвЖЈРэЃЌНЋгаЙиЪ§ОнДњШыЧѓНтМДПЩЃЛ
ЃЈ2ЃЉдкЁїABCжаЃЌЗжБ№ЧѓЕУBCЕФГЄКЭШ§ИіФкНЧЕФЖШЪ§ЃЌРћгУЬтФПжазмНсЕФе§ЯвЖЈРэЧѓACЕФГЄМДПЩЃЎ
ЃЈ1ЃЉгЩе§аўЖЈРэЕУЃКЁЯAЃН60ЁуЃЌACЃН20![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК60ЁуЃЌ20![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЃК
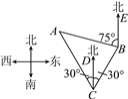
вРЬтвтЃЌЕУBCЃН40ЁС0.5ЃН20(КЃРя)ЃЎ
ЁпCDЁЮBEЃЌ
ЁрЁЯDCBЃЋЁЯCBEЃН180Ёу.
ЁпЁЯDCBЃН30ЁуЃЌЁрЁЯCBEЃН150Ёу.
ЁпЁЯABEЃН75ЁуЃЌЁрЁЯABCЃН75ЁуЃЌ
ЁрЁЯAЃН45Ёу.
дкЁїABCжаЃЌ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУABЃН10![]() Ёж24.49(КЃРя)ЃЎ
Ёж24.49(КЃРя)ЃЎ
Д№ЃКгцеўДЌОрКЃЕКAЕФОрРыABдМЮЊ24.49КЃРяЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯA=40ЁуЃЌЁїABCЕФЭтНЧЁЯCBDЕФЦНЗжЯпBEНЛACЕФбгГЄЯпгкЕуEЃЎ
ЃЈ1ЃЉЧѓЁЯCBEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDFЁЮBEЃЌНЛACЕФбгГЄЯпгкЕуFЃЌЧѓЁЯFЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌИУаЁзщЗЂЯж8УзИпЦьИЫDEЕФгАзгEFТфдкСЫАќКЌвЛдВЛЁаЭаЁЧХдкФкЕФТЗЩЯЃЌгкЪЧЫћУЧПЊеЙСЫВтЫуаЁЧХЫљдкЭМЕФАыОЖЕФЛюЖЏЁЃаЁИеЩэИп1.6УзЃЌВтЕУЦфгАГЄЮЊ2.4УзЃЌЭЌЪБВтЕУEGЕФГЄЮЊ3УзЃЌHFЕФГЄЮЊ1УзЃЌВтЕУЙАИпЃЈЛЁGHЕФжаЕуЕНЯвGHЕФОрРыЃЌМДMNЕФГЄЃЉЮЊ2УзЃЌЧѓаЁЧХЫљдкдВЕФАыОЖЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙЄвеУРЪѕжаЃЌГЃашЩшМЦЖдГЦЭМАИЃЎдкШчЭМЕФе§ЗНаЮЭјИёжаЃЌЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЎЧыдкЭМжадйеввЛИіИёЕу
ЃЎЧыдкЭМжадйеввЛИіИёЕу![]() ЃЌЪЙЫќгывбжЊЕФ
ЃЌЪЙЫќгывбжЊЕФ![]() ИіИёЕузщГЩжсЖдГЦЭМаЮЃЌдђЕу
ИіИёЕузщГЩжсЖдГЦЭМаЮЃЌдђЕу![]() ЕФзјБъЮЊ________ЃЈШчЙћТњзуЬѕМўЕФЕу
ЕФзјБъЮЊ________ЃЈШчЙћТњзуЬѕМўЕФЕу![]() ВЛжЙвЛИіЃЌЧыНЋЫќУЧЕФзјБъЖМаДГіРДЃЉЃЎ
ВЛжЙвЛИіЃЌЧыНЋЫќУЧЕФзјБъЖМаДГіРДЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪаЗРбДжИЛгВПОіЖЈЖдФГЫЎПтЕФЫЎАгНјааМгИпМгЙЬЃЌЩшМЦЪІЬсЙЉЕФЗНАИЪЧЃКЫЎАгМгИп1Уз(EFЃН1Уз)ЃЌБГЫЎЦТAFЕФЦТЖШiЃН1ЁУ1ЃЌвбжЊABЃН3УзЃЌЁЯABEЃН120ЁуЃЌЧѓЫЎАгдРДЕФИпЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ЉЃЈxЉhЃЉ2ЃЈhЮЊГЃЪ§ЃЉЃЌЕБздБфСПxЕФжЕТњзу2ЁмxЁм5ЪБЃЌгыЦфЖдгІЕФКЏЪ§жЕyЕФзюДѓжЕЮЊЉ1ЃЌдђhЕФжЕЮЊЃЈ ЃЉ
A. 3Лђ6 B. 1Лђ6 C. 1Лђ3 D. 4Лђ6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABгыxжсНЛгкЕуAЃЈ1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЈ0ЃЌЉ2ЃЉЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєжБЯпABЩЯЕФЕуCдкЕквЛЯѓЯоЃЌЧвSЁїBOC=2ЃЌЧѓОЙ§ЕуCЕФЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈaЃЌ0ЃЉЃЌBЃЈ0ЃЌbЃЉЃЌЧв|a+4|+b2Љ86+16ЃН0ЃЎ

ЃЈ1ЃЉЧѓaЃЌbЕФжЕЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌcЮЊyжсИКАыжсЩЯвЛЕуЃЌСЌCAЃЌЙ§ЕуCзїCDЁЭCAЃЌЪЙCDЃНCAЃЌСЌBDЃЎЧѓжЄЃКЁЯCBDЃН45ЁуЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєгавЛЕШбќRtЁїBMNЃЌЁЯBMNЃН90ЁуЃЌСЌANЃЌШЁANжаЕуPЃЌСЌPMЁЂPOЃЎЪдЬНОПPMКЭPOЕФЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
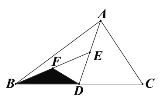
ЁОЬтФПЁПШчЭМЃЌDЁЂEЁЂFЗжБ№ЮЊBCЁЂADЁЂBEЕФжаЕуЃЌШєЁїBFDЕФУцЛ§ЮЊ6ЃЌдђ ЁїABCЕФУцЛ§ЕШгк_____________.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com