
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求经过点C的反比例函数的解析式.

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=45°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,CF⊥AC交AB的延长线于点F,G为BC的中点,射线AG交CF于D,E在CF上,CE=AD,连接BD,BE.求证:△BDE是等边三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”(译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?)若买得公鸡和母鸡之和不超过20只,且买得公鸡数不低于母鸡数,则此时买得小鸡_____只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.

(1)试求证图(1)中:∠BAE=∠DEF;
(2)当点E在线段BD上移动时,如图(1)所示,求证:AE=EF;
(3)当点E在直线BD上移动时,在图(2)与图(3)中,分别猜想线段AE与EF有怎样的数量关系,并就图(3)的猜想结果说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,以斜边
,以斜边![]() 的中点
的中点![]() 为旋转中心,把这个三角形按逆时针方向旋转
为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转后两个直角三角形重叠部分的面积为( )
,则旋转后两个直角三角形重叠部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )
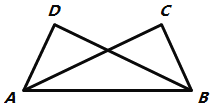
A.AD=BC,BD=ACB.AD=BC,∠BAD=∠ABC
C.BD=AC,∠DBA=∠CABD.AD=BC,∠D=∠C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com