
下列一元二次方程有两个相等实数根的是( )
A.x2﹣2x+1=0 B. 2x2﹣x+1=0 C. 4x2﹣2x﹣3=0 D. x2﹣6x=0
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
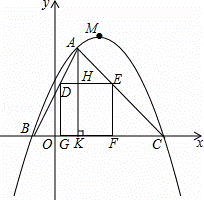
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
| x | … | ﹣2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
(1)求出这条抛物线的解析式;
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
问题:如图(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,试探究AD、DE、EB满足的等量关系.
[探究发现]
小聪同学利用图形变换,将△CAD绕点C逆时针旋转90°得到△CBH,连接EH,由已知条件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.
根据“边角边”,可证△CEH≌ ,得EH=ED.
在Rt△HBE中,由 勾股 定理,可得BH2+EB2=EH2,由BH=AD,可得AD、DE、EB之间的等量关系是 .
[实践运用]
(1)如图(2),在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数;
(2)在(1)条件下,连接BD,分别交AE、AF于点M、N,若BE=2,DF=3,BM=2 ,运用小聪同学探究的结论,求正方形的边长及MN的长.
,运用小聪同学探究的结论,求正方形的边长及MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
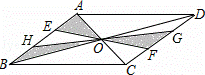
如图,▱ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向▱ABCD内部投掷飞镖(每次均落在▱ABCD内,且落在▱ABCD 内任何一点的机会均等)恰好落在阴影区域的概率为( )
内任何一点的机会均等)恰好落在阴影区域的概率为( )
A.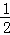 B.
B. 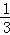 C.
C. 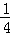 D.
D. 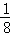
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为 米.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
A. 掷一枚硬币,正面一定朝上
B. 某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C. 旅客上飞机前的安检应采用抽样调查
D. 方差越大,数据的波动越大
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据: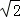 ≈1.41,
≈1.41,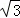 ≈1.73)
≈1.73)
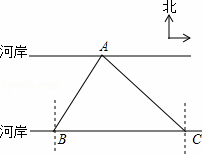
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com