
����Ŀ��ij����ѧУҪ��ʥ���ھ��л㱨�ݳ�����Ҫ��һЩʥ��ñ��Ϊ������ѧ���Ķ���������ѧУ�����Լ�������Щʥ��ñ�����ʥ��ñ(Բ��״)�Ĺ����ĸ�߳�Ϊ42���ף�����ֱ��Ϊ16����.
(1)��ʥ��ñ�IJ���չ��ͼ(����)��Բ�ĽǵĶ���(��ȷ��1��)��
(2)��֪A�ֹ���ֽƬ����3��ʥ��ñ��B�ֹ���ֽƬ����4��ʥ��ñ���㱨�ݳ���Ҫ26��ʥ��ñ��д��A�ֹ���ֽƬ![]() (��)��B�ֹ���ֽƬ
(��)��B�ֹ���ֽƬ![]() (��)֮��ĺ�����ϵʽ��
(��)֮��ĺ�����ϵʽ��![]() �����ֵ����Сֵ�����Լ�����ʱ��A��B���ֹ���ֽƬ���������ʱ���Ų����˷�ֽ�ţ�
�����ֵ����Сֵ�����Լ�����ʱ��A��B���ֹ���ֽƬ���������ʱ���Ų����˷�ֽ�ţ�
���𰸡�(1) ![]() .(2) A��B���ֹ���ֽƬ����6�š�2�Ż�2�š�5��ʱ���Ų����˷�ֽ��.
.(2) A��B���ֹ���ֽƬ����6�š�2�Ż�2�š�5��ʱ���Ų����˷�ֽ��.
��������
��1������Բ�Ļ���=Բ�ĵ����ܳ��ɵ�Բ�ĽǵĶ�����
��2������26��ʥ��ñ�ĸ����г���Ӧ�ĵ�����ϵ���ɵ�y��x֮��ĺ�����ϵʽ��Ȼ��ȡ������������ֵ����Сֵ����.
(1)�ߵ���ֱ��Ϊ16���ף�
��Բ�ĵ����ܳ�Ϊ![]() ���ף�
���ף�
��ʥ��ñ�IJ���չ��ͼ��һ�����Σ�
�����εĻ�����![]() ��
��
�����ε�Բ�Ľ�Ϊ![]() ����
����![]() ��
��
���![]() �������ε�Բ�Ľ�Լ��
�������ε�Բ�Ľ�Լ��![]() .
.
(2)![]() ����
����![]() ����
����![]() �����ֵ��
�����ֵ��![]() ����Сֵ��0.
����Сֵ��0.
��Ȼ��![]() ����ȡ�������Ų����˷�ֽ�ţ�
����ȡ�������Ų����˷�ֽ�ţ�
��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ����A��B���ֹ���ֽƬ����6�š�2�Ż�2�š�5��ʱ���Ų����˷�ֽ��.
����A��B���ֹ���ֽƬ����6�š�2�Ż�2�š�5��ʱ���Ų����˷�ֽ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
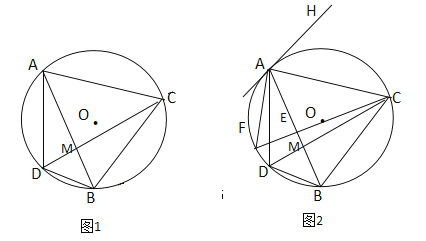
����Ŀ����ͼ1����֪��O����ADB�����Բ����ADB��ƽ����DC��AB�ڵ�M������O�ڵ�C������AC��BC.
��1����֤��AC=BC��
��2����ͼ2����ͼ1 �Ļ���������O��ֱ��CF��AB�ڵ�E������AF������A����O������AH����AH//BC�����ACF�Ķ�����
��3���ڣ�2���������£�����ABD�����Ϊ![]() ����ABD����ABC�������Ϊ2��9����CD�ij�.
����ABD����ABC�������Ϊ2��9����CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
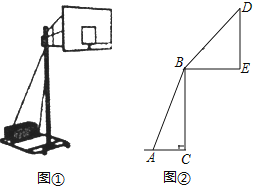
����Ŀ����ͼ�٣��ڷֱ���ij������ܵ�ʵ��ͼ��ʾ��ͼ����֪֧��AB�ij�Ϊ2.3m��֧��AB�����ļнǡ�BAC��70����BE�ij�Ϊ1.5m�����岿֧��BD��ˮƽ֧��BE�ļн�Ϊ46����BC��DE��ֱ�ڵ��棬�����嶥��D������ľ��룮(�������һλС�����ο����ݣ�sin70���0.94��cos70���0.34��tan70���2.75��sin46���0.72��cos46���0.69��tan46���1.04)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
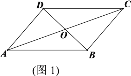
����Ŀ�����ǰ������߶�Ӧ��ȣ��Ҽнǻ���(�����)�����������ν���������������������ͼ1����ABCD�У���AOB����BOC����������������.
(1)д��ͼ1������һ����������������_______��
(2)��ͼ2�У��ó߹�����һ����EFH��ʹ����EFH����EFGΪ��������������������EFH����EFG��EFͬ�࣬��֤����һ������������������������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
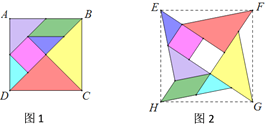
����Ŀ�����ɰ����������ȵ�һ��Խ���죬����������Ϊ������ħ���������������ͼ�����Σ���ͼ1�������糵��������ͼ2��������ͬһ�����ɰ�ƴ�ɵģ���ͼ��������ABCD��EFGH�������Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��Ҷ��˴�ѧУ����ȥ�»���꿴�飬�ײ���һ��ʱ����������г�����ͬ·���н����˾�����ǰ�У�����֮��ľ���s(��)��׳���ʱ��t(��)֮��ĺ�����ϵ��ͼ��ʾ������˵���������( )
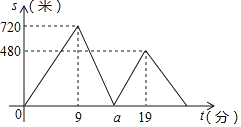
A. �ҵ��ٶ��Ǽ��ٶȵ�2.5��
B. a��15
C. ѧУ���»���깲3800��
D. ��25���ӵ����»����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
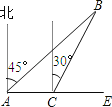
����Ŀ����ͼ��ʾ���ס�������ͬʱ�ɸۿ�A������������B���״��ض���������B���У����ٶ�Ϊ15����/Сʱ���Ҵ��ٶ�Ϊ20����/Сʱ����������������1Сʱ����C�ۿڽ��ÿͣ�ͣ����Сʱ����ת��ƫ��30�㷽����B�������ٶ���Ϊ20����/Сʱ��
��1����ۿ�A������B�ľ��룻
��2��B������һ�����������������Բ5�����ڶ����Կ����������ʼס���������һ���ȿ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
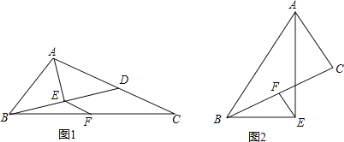
����Ŀ����ͼ������ABC�У�AEƽ�֡�BAC��BE��AE�ڵ�E����F��BC���е㣮
��1����ͼ1��BE���ӳ�����AC���ཻ�ڵ�D����֤��EF=![]() ��AC��AB����
��AC��AB����
��2����ͼ2����ֱ��д���߶�AB��AC��EF֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
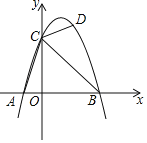
����Ŀ����ͼ����֪���κ���y����x2+2x+3��ͼ����x���ཻ�ڵ�A��B����y���ཻ�ڵ�C������AC��BC���ú����ڵ�һ�����ڵ�ͼ�����Ƿ����һ��D��ʹ��CBƽ�֡�ACD�������ڣ����D�����꣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com