Question

【题目】如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°.

（1）利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD（保留作图痕迹，不写作法）

（2）在（1）所作的图形中，求AB与CD的比值．

Answer 1

【答案】（1）画图见解析；

（2）．

【解析】【试题分析】（1）尺规作图，作一个角的平分线；（2）如图2，连接OD，设⊙O的半径为r，因为AC是⊙O的直径，∴∠ABC=90°.．

在Rt△ACB中，∠ACB=30°，根据30度的直角边是斜边的一半，AB=AC=r．

由于BD是∠ABC的平分线，根据角平分线的定义得，∠ABD=∠CBD=45° ．

根据同弧所对的圆周角是圆心角的一半，得∠DOC=2∠CBD =90°

在Rt△ODC中，DC= =r．则．

【试题解析】

（1）如图所示；

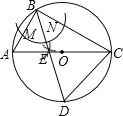
（2）如图2，连接OD，设⊙O的半径为r，

∵AC是⊙O的直径，∴∠ABC=90°.．

在Rt△ACB中，∠ACB=30°，

∴AB= AC=r．

∵BD是∠ABC的平分线，∴∠ABD=∠CBD=45° ．

∴∠DOC=2∠CBD =90°

在Rt△ODC中，DC= =r．

∴．