Question

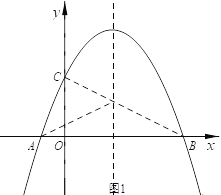
【题目】如图，抛物线经过A（﹣1，0），B（3，0），C（0， ）三点．

（1）求抛物线的解析式；

（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线的解析式为： ；

（2）P（1，1）；

（3）存在，点N的坐标为（2， ），（， ），（， ）．

【解析】【试题分析】

（1）设抛物线的解析式为y=ax2+bx+c（a≠0），因为A（﹣1，0），B（5，0），C（0， ）三点在抛物线上，则构造三元方程组，得，解得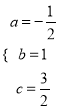．即抛物线的解析式为： ；

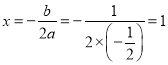（2）如图1，根据抛物线的解析式为，得其对称轴为直线： ，连接BC，设直线BC的解析式为，

根据B、C两点，得方程组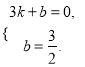解得

即直线BC的解析式为，当x=1时， .∴P（1，1）；

（3）存在．A（﹣1，0），C（0， ）,M(m,0), ,根据相对的两个点的中点坐标重合.

若A、C相对，则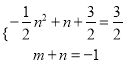 ，解得n=2, ∴N1（2， ）；

若A、M相对，则，解得n= ∴N2（， ），N3（， ）．；

若A、N相对，则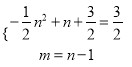 ，解得n=2,（舍去）；

综上所述，点N的坐标为（2， ），（， ），（， ）．

【试题解析】

（1）设抛物线的解析式为y=ax2+bx+c（a≠0），

∵A（﹣1，0），B（5，0），C（0， ）三点在抛物线上，

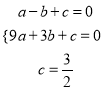∴，解得．

∴抛物线的解析式为： ；

（2）∵抛物线的解析式为，

∴其对称轴为直线： .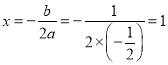

连接BC，设直线BC的解析式为，

∵B（3，0），C（0， ），∴解得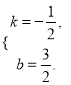

∴直线BC的解析式为

当x=1时， .∴P（1，1）；

（3）存在．

存在．A（﹣1，0），C（0， ）,M(m,0),

若A、C相对，则 ，解得n=2, ∴N1（2， ）；

若A、M相对，则，解得n= ∴N2（， ），N3（， ）．；

若A、N相对，则 ，解得n=2,（舍去）；

综上所述，点N的坐标为（2， ），（， ），（， ）．