
【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠B=70°,∠C=40°,求∠DAE的度数.
(2)若∠B﹣∠C=30°,则∠DAE= .
(3)若∠B﹣∠C=α(∠B>∠C),求∠DAE的度数(用含α的代数式表示)

【答案】(1)15°;(2)15°;(3)![]() α;
α;
【解析】
(1)根据角平分线的定义和互余进行计算;
(2)根据三角形内角和定理和角平分线定义得出∠DAE的度数等于∠B与∠C差的一半解答即可;
(3)根据(2)中所得解答即可.
解:∵AD⊥BC于D,
∴∠ADC=90°,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC,
∠BAC,
而∠BAC=180°﹣∠B﹣∠C,
∴∠EAC=90°﹣![]() ∠B﹣
∠B﹣![]() ∠C,
∠C,
∵∠DAC=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣∠C﹣[90°﹣![]() ∠B﹣
∠B﹣![]() ∠C]
∠C]
=![]() (∠B﹣∠C),
(∠B﹣∠C),
(1)若∠B=70°,∠C=40°,则∠DAE=![]() (70°﹣40°)=15°;
(70°﹣40°)=15°;
(2)若∠B﹣∠C=30°,则∠DAE=![]() ×30°=15°;
×30°=15°;
(3)若∠B﹣∠C=α(∠B>∠C),则∠DAE=![]() α;
α;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明为班级联欢会设计了一个摸球游戏.游戏规则如下:在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.游戏者先从纸箱里随机摸出一个球,记录颜色后放回,将小球摇匀,再随机摸出一个球,若两次摸到的球颜色相同,则游戏者可获得一份纪念品.请你利用树状图或列表法求游戏者获得纪念品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,点D是边BC上一动点,以AD为直角边作等腰直角△ADE,分别过A、E点向BC边作垂线,垂足分别为F、G.连接BE.
(1)证明:BG=FD;
(2)求∠ABE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
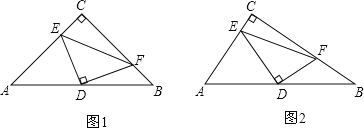
【题目】已知:如图1,Rt△ABC中,∠ACB=90°,D为AB中点,DE、DF分别交AC于E,交BC于F,且DE⊥DF.
(1)如果CA=CB,求证:AE2+BF2=EF2;
(2)如图2,如果CA<CB,(1)中结论还能成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: 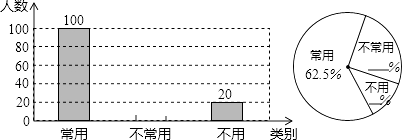
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com