
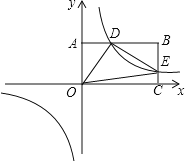
【题目】如图,反比例函数![]() (k>0)与长方形OABC在第一象限相交于D,E两点,OA=2,OC=4,连结OD、OE、DE.记△OAD、△OCE的面积分别为
(k>0)与长方形OABC在第一象限相交于D,E两点,OA=2,OC=4,连结OD、OE、DE.记△OAD、△OCE的面积分别为![]() 、
、![]() .当
.当![]() =2时,求k的值及点D、E的坐标,试判断△ODE的形状.
=2时,求k的值及点D、E的坐标,试判断△ODE的形状.
科目:初中数学 来源: 题型:
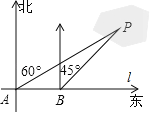
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物业公司计划对所管理的小区3000m2区域进行绿化,经投标由甲、乙两个工程队来完成,甲、乙两个工程队每天共完成绿化面积150m2,甲队完成600m2区域的绿化面积与乙队完成300m2区域的绿化面积所用的天数相同.
(1)求甲、乙两个工程队每天各能完成多少面积的绿化?
(2)若甲队每天绿化费用是0.6万元,乙队每天绿化费用是0.2万元,该物业公司要使这次绿化总费用不超过17万元,则至少安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1的解析式为![]() ,直线l2的解析式为
,直线l2的解析式为![]() ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
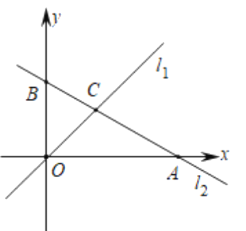

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2﹣9(其中a>0)上,AB∥x轴,点P是抛物线的顶点,tan∠PBA=2,∠BAC=45°.
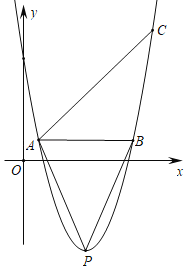
(1)填空:抛物线的顶点P的坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为10,当2m﹣3≤x≤2m+5时,y的最小值为5,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
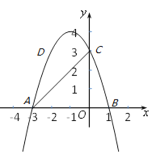
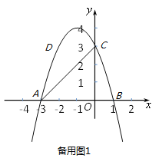
【题目】如图,抛物线与x轴相交于点A(-3,0)、点B(1,0),与y轴交于点C(0,3),点D是第二象限内抛物线上一动点.F点坐标为(-4,0).
(1)求这条抛物线的解析式;并写出顶点坐标;
(2)当D为抛物线的顶点时,求△ACD的面积;
(3)连接OD交线段AC于点E.当△AOE与△ABC相似时,求点D的坐标;
(4)在x轴上方作正方形AFMN,将正方形AFMN沿x轴下方向向右平移t个单位,其中0≤t≤4,设正方形AFMN与△ABC的重叠总分面积为S,直接写出S关于t的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
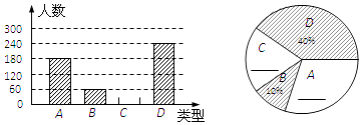
请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
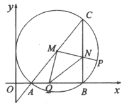
【题目】如图,在平面直角坐标系![]() 中,与y轴相切的
中,与y轴相切的![]() 与x轴交于A、B两点,AC为
与x轴交于A、B两点,AC为![]() 直径,
直径,![]() ,
,![]() ,连结BC,点P为劣弧
,连结BC,点P为劣弧![]() 上点,点Q为线段AB上点,且
上点,点Q为线段AB上点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则当 NQ平分
,则当 NQ平分![]() 时,点P坐标是________.
时,点P坐标是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com